题目内容
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,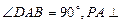 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=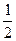 AB=1,M是PB的中点。
AB=1,M是PB的中点。
(1)求直线AC与PB所成角的余弦值;
(2)求面AMC与面PMC所成锐二面角的大小的余弦值。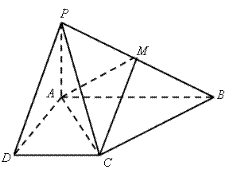
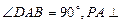 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=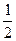 AB=1,M是PB的中点。
AB=1,M是PB的中点。(1)求直线AC与PB所成角的余弦值;
(2)求面AMC与面PMC所成锐二面角的大小的余弦值。

(1)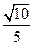
(2)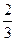
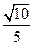
(2)
因为PA⊥PD,PA⊥AB,AD⊥AB,以A为坐标原点AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,不妨设AD=1,则各点坐标为A(0,0,0)B(0,2,0),
C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,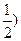 …2分
…2分
(1)解:因
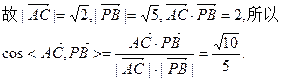 …6分
…6分
(2)解:由题得:平面PMC的法向量为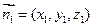
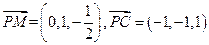
所以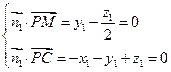 解得:
解得: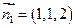 ….9分
….9分
同理设平面AMC的法向量为
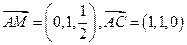
所以 解得:
解得: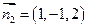 ….12分
….12分
故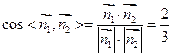 , 即所求锐二面角的余弦值为
, 即所求锐二面角的余弦值为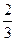 …..14分
…..14分
注:几何法求解,相应分步给分。
C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,
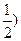 …2分
…2分(1)解:因
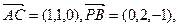
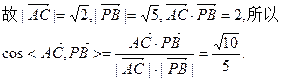 …6分
…6分(2)解:由题得:平面PMC的法向量为
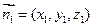
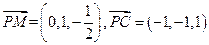
所以
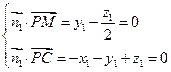 解得:
解得: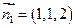 ….9分
….9分同理设平面AMC的法向量为

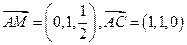
所以
 解得:
解得: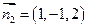 ….12分
….12分故
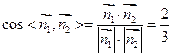 , 即所求锐二面角的余弦值为
, 即所求锐二面角的余弦值为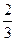 …..14分
…..14分注:几何法求解,相应分步给分。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
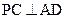 ,
, ,
,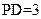 ,
,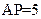 .
.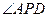 是直线
是直线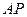 与平面
与平面 所成的角
所成的角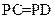 ,求二面角
,求二面角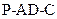 的余弦值.
的余弦值.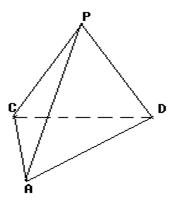
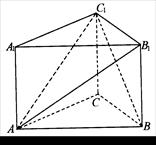
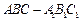 中,
中,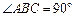 ,
,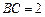 ,
,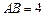 ,
,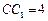 ,E在
,E在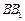 上,且
上,且 ,
,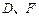 分别为
分别为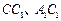 的中点.
的中点.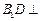 平面
平面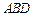 ;
;  与
与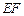 所成的角;
所成的角;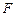 到平面
到平面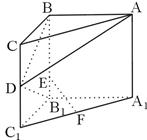
 平面
平面 是正三角形,
是正三角形, 。
。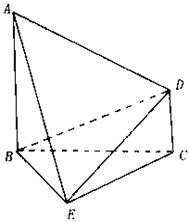
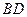 与
与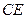 所成角的余弦值;
所成角的余弦值;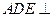 平面
平面 ;
; 的余弦值。
的余弦值。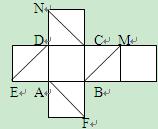
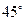 圈上有A,B两地分别是东经
圈上有A,B两地分别是东经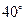 和西经
和西经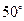 ,若设地球半径为R,则A, B的球面距离为
,若设地球半径为R,则A, B的球面距离为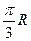 B
B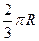 C
C 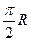 D R
D R 表示直线,
表示直线,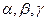 表示平面):
表示平面):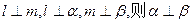 ;② 若
;② 若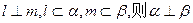 ;
;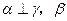 ∥
∥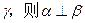 ;④ 若
;④ 若 ∥
∥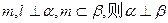 .
.