题目内容
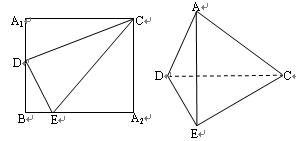
(本小题满分12分)如图,P是平面ADC外的一点,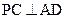 ,
, ,
,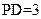 ,
,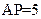 .
.
(1)求证: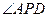 是直线
是直线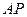 与平面
与平面 所成的角
所成的角
(2)若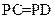 ,求二面角
,求二面角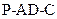 的余弦值.
的余弦值.
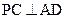 ,
, ,
,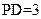 ,
,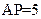 .
.(1)求证:
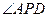 是直线
是直线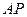 与平面
与平面 所成的角
所成的角(2)若
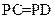 ,求二面角
,求二面角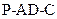 的余弦值.
的余弦值.
(1)证明见解析
(2)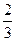
(2)
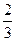
(1)在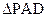 中,
中,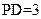 ,
,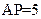 ,
,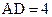 ,
,
∴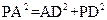 ,∴
,∴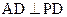 ,………3分
,………3分
又因为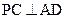 ,所以
,所以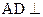 平面
平面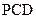 ……5分
……5分
∴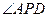 是直线
是直线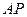 与平面
与平面 所成的角……………6分
所成的角……………6分
(2)解法一:由(1)得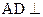 平面
平面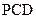 ,则
,则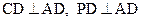 ……………………………8分
……………………………8分
又∵平面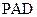
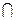 平面
平面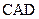 =
=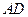 ,∴
,∴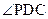 是二面角
是二面角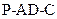 的平面角………9分
的平面角………9分
在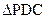 中,
中,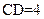 ,
,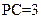 ,
,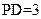
由余弦定理得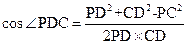 =
=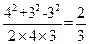
所以,求二面角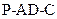 的余弦值为
的余弦值为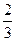 ………12分
………12分
解法二:过点P作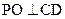 于点O,由(1)知
于点O,由(1)知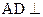 平面
平面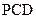 ,
,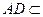 平面
平面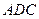
∴平面PCD⊥平面CDA,则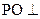 平面
平面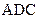 .……………7分
.……………7分
∵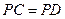 , ∴
, ∴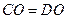 ………………………………8分
………………………………8分
则以O为原点建立如图所示的直角坐标系O-XYZ.
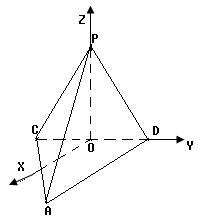
∴O(0,0,0),A(4,2,0),D(0,2,0),P(0,0,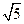 ),C(0,-2,0) ……9分
),C(0,-2,0) ……9分
设平面PAD的法向量为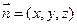 .
.
∴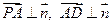 ,又
,又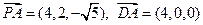
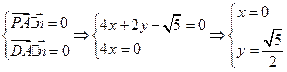 ,所以
,所以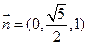 ……………10分
……………10分
又因为平面ACD的法向量为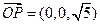 ……………11分
……………11分
∴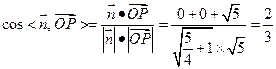
因为二面角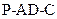 为锐角,则二面角
为锐角,则二面角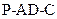 的余弦值是
的余弦值是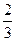 …………12分
…………12分
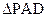 中,
中,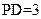 ,
,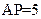 ,
,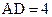 ,
,∴
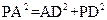 ,∴
,∴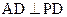 ,………3分
,………3分又因为
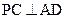 ,所以
,所以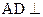 平面
平面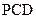 ……5分
……5分∴
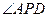 是直线
是直线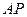 与平面
与平面 所成的角……………6分
所成的角……………6分(2)解法一:由(1)得
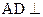 平面
平面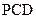 ,则
,则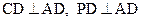 ……………………………8分
……………………………8分又∵平面
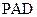
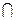 平面
平面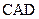 =
=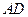 ,∴
,∴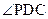 是二面角
是二面角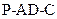 的平面角………9分
的平面角………9分在
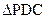 中,
中,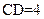 ,
,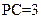 ,
,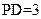
由余弦定理得
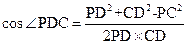 =
=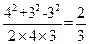
所以,求二面角
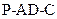 的余弦值为
的余弦值为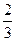 ………12分
………12分解法二:过点P作
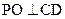 于点O,由(1)知
于点O,由(1)知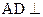 平面
平面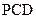 ,
,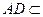 平面
平面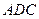
∴平面PCD⊥平面CDA,则
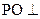 平面
平面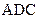 .……………7分
.……………7分∵
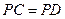 , ∴
, ∴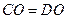 ………………………………8分
………………………………8分则以O为原点建立如图所示的直角坐标系O-XYZ.

∴O(0,0,0),A(4,2,0),D(0,2,0),P(0,0,
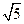 ),C(0,-2,0) ……9分
),C(0,-2,0) ……9分设平面PAD的法向量为
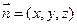 .
.∴
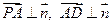 ,又
,又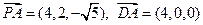
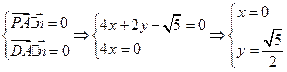 ,所以
,所以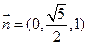 ……………10分
……………10分又因为平面ACD的法向量为
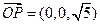 ……………11分
……………11分∴
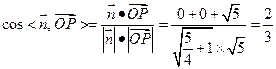
因为二面角
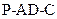 为锐角,则二面角
为锐角,则二面角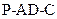 的余弦值是
的余弦值是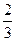 …………12分
…………12分
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
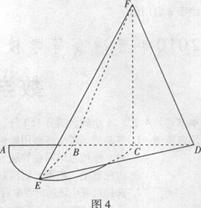
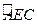 是半径为
是半径为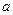 的半圆,
的半圆,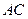 为直径,点
为直径,点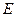 为
为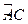 的中点,点
的中点,点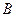 和点
和点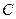 为线段
为线段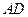 的三等分点,平面
的三等分点,平面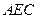 外一点
外一点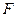 满足
满足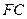
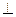 平面
平面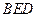 ,
,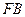 =
=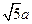 .
. 
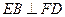 ;
; 的距离.
的距离. 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=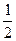 AB=1,M是PB的中点。
AB=1,M是PB的中点。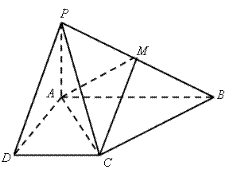
 和两条异面直线都平行的直线(
和两条异面直线都平行的直线(  )
)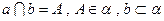
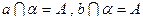
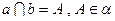
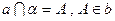
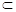 α,则l∥β
α,则l∥β