题目内容
(本小题满分12分)如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=BC=CC1=2.
(I)证明:AB1⊥BC1;
(II)求点B到平面AB1C1的距离;
(III)求二面角C1—AB1—A1的大小.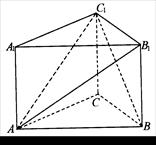
(I)证明:AB1⊥BC1;
(II)求点B到平面AB1C1的距离;
(III)求二面角C1—AB1—A1的大小.

(I)证明见解析
(II)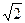
(III)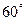
(II)
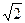
(III)
(法一)
(1)证:连B1C ∵平面ABC⊥平面BCC1B1
又AC⊥BC ∴AC⊥面BCC1B1 ∴B1C为AB1在面BCC1B1内的射影
又BC=BB1 ="2" ∴四边形BCC1B1为正方形
∴四边形BCC1B1为正方形
∴B1C ⊥ BC1 ∴AB1⊥ BC1 …………………………………………………4分
(2)∵BC∥B1C1
 ∴C到面AB1C1的距离即为B到面AB1C1的距离
∴C到面AB1C1的距离即为B到面AB1C1的距离
∵平面A1B1C1⊥平面ACC1A1
又B1C1⊥A1C1 ∴B1C1⊥平面ACC1A1∴平面AB1C1⊥平面ACC1A1
连A1C∩AC1 ="O"
∵四边形ACC1A1为正方形 ∴CO⊥面AB1C1
∴CO即为所求 ∴CO=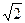 ∴B到面AB1C1
∴B到面AB1C1 的距离为
的距离为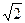 ………………………8分
………………………8分
(3)由(2)得 A1O⊥面AB1C1
过O做OE⊥AB1于E 连A1E 由三垂线定理有A1E⊥AB1
∴∠A1EO为二面角C1-AB1-A1的平面角
又在Rt⊿A1OE中,A1 O=
O=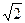 OE=
OE=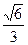
∴tan∠A1EO=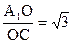 ∴∠A1EO=
∴∠A1EO=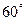
∴二面角C1-AB1-A1的大小为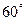 …………………………………………12分
…………………………………………12分
(法二)(1)建立直角坐标系,其中C为坐标原点.
依题意A(2,0,0),B(0,2,0),B1(0,2,2),
C1(0,0,2),因为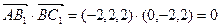 ,所以A
,所以A B1⊥BC1. ……………4分
B1⊥BC1. ……………4分
(2)设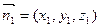 是平面AB1C1的法向量,
是平面AB1C1的法向量,
由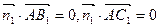 得
得
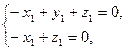 所以
所以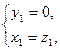 令
令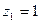 ,则
,则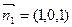 ,
,
因为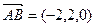 ,所以,B到平面AB1
,所以,B到平面AB1 C1的距离为
C1的距离为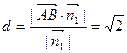 .……………8分
.……………8分
(3)设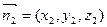 是平面A1AB1的法向量.由
是平面A1AB1的法向量.由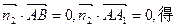
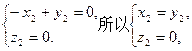 令
令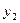 =1,
=1,
则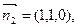
因为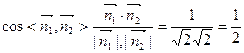 所以,二面角C1—AB1—A1的大小为60°…
所以,二面角C1—AB1—A1的大小为60°… 12分
12分
(1)证:连B1C ∵平面ABC⊥平面BCC1B1
又AC⊥BC ∴AC⊥面BCC1B1 ∴B1C为AB1在面BCC1B1内的射影
又BC=BB1 ="2"
 ∴四边形BCC1B1为正方形
∴四边形BCC1B1为正方形∴B1C ⊥ BC1 ∴AB1⊥ BC1 …………………………………………………4分
(2)∵BC∥B1C1
 ∴C到面AB1C1的距离即为B到面AB1C1的距离
∴C到面AB1C1的距离即为B到面AB1C1的距离∵平面A1B1C1⊥平面ACC1A1
又B1C1⊥A1C1 ∴B1C1⊥平面ACC1A1∴平面AB1C1⊥平面ACC1A1
连A1C∩AC1 ="O"
∵四边形ACC1A1为正方形 ∴CO⊥面AB1C1
∴CO即为所求 ∴CO=
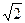 ∴B到面AB1C1
∴B到面AB1C1 的距离为
的距离为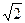 ………………………8分
………………………8分(3)由(2)得 A1O⊥面AB1C1
过O做OE⊥AB1于E 连A1E 由三垂线定理有A1E⊥AB1
∴∠A1EO为二面角C1-AB1-A1的平面角
又在Rt⊿A1OE中,A1
 O=
O=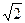 OE=
OE=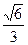
∴tan∠A1EO=
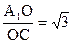 ∴∠A1EO=
∴∠A1EO=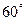
∴二面角C1-AB1-A1的大小为
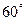 …………………………………………12分
…………………………………………12分(法二)(1)建立直角坐标系,其中C为坐标原点.
依题意A(2,0,0),B(0,2,0),B1(0,2,2),
C1(0,0,2),因为
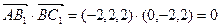 ,所以A
,所以A B1⊥BC1. ……………4分
B1⊥BC1. ……………4分 (2)设
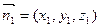 是平面AB1C1的法向量,
是平面AB1C1的法向量,由
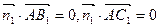 得
得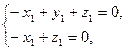 所以
所以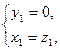 令
令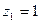 ,则
,则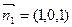 ,
,因为
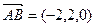 ,所以,B到平面AB1
,所以,B到平面AB1 C1的距离为
C1的距离为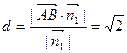 .……………8分
.……………8分(3)设
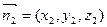 是平面A1AB1的法向量.由
是平面A1AB1的法向量.由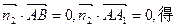
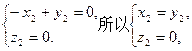 令
令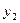 =1,
=1,则
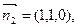
因为
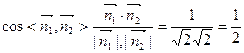 所以,二面角C1—AB1—A1的大小为60°…
所以,二面角C1—AB1—A1的大小为60°… 12分
12分
练习册系列答案
相关题目
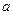 ,D为BC中点,M在BB1上,且
,D为BC中点,M在BB1上,且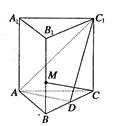
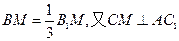 .
.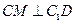 ;
;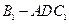 的体积.
的体积.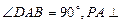 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=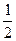 AB=1,M是PB的中点。
AB=1,M是PB的中点。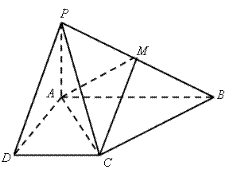
 ,
,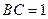 ,设AE与平面ABC所成的角为
,设AE与平面ABC所成的角为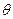 ,且
,且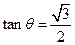 ,
,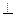 平面ABC.
平面ABC.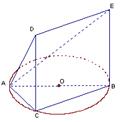
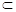 α,则l∥β
α,则l∥β 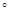 的二面角,这时A到边BC的距离是( )
的二面角,这时A到边BC的距离是( )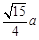
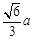
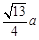
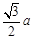
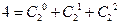 ,
,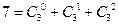 ,
,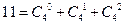 ;……
;……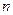 条直线将一个平面最多分成多少个部分(
条直线将一个平面最多分成多少个部分(