题目内容
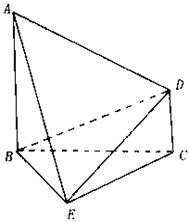
如图,已知 平面
平面 是正三角形,
是正三角形, 。
。
(Ⅰ)求异面直线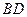 与
与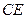 所成角的余弦值;
所成角的余弦值;
(Ⅱ)求证:平面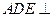 平面
平面 ;
;
(Ⅲ)求二面角 的余弦值。
的余弦值。
 平面
平面 是正三角形,
是正三角形, 。
。
(Ⅰ)求异面直线
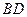 与
与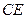 所成角的余弦值;
所成角的余弦值;(Ⅱ)求证:平面
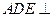 平面
平面 ;
;(Ⅲ)求二面角
 的余弦值。
的余弦值。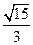
解:(Ⅰ)当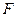 为
为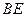 的中点时,
的中点时,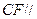 平面
平面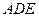 ………………………………1分
………………………………1分
证明:取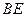 的中点
的中点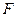 、
、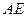 的中点
的中点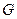 ,连结
,连结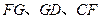
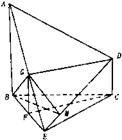
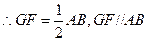
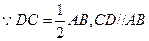 B
B
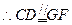
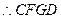 是平行四边形……………………3分
是平行四边形……………………3分
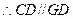
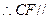 平面
平面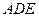 …………………………4分
…………………………4分
(Ⅱ)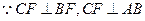
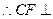 平面
平面
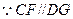
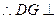 平面
平面 ……………………………………………………………………6分
……………………………………………………………………6分
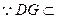 平面
平面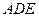
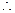 平面
平面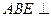 平面
平面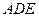 ……………………………………………………………7分
……………………………………………………………7分
(Ⅲ)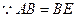
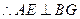
 平面
平面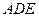
过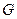 作
作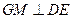 ,连结
,连结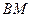 ,则
,则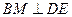
则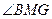 为二面角
为二面角 的平面角………………………………………9分
的平面角………………………………………9分
设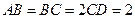 ,则
,则
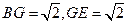
在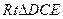 中,
中,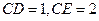
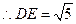
又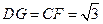
由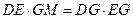 得
得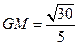 …………………………………………11分
…………………………………………11分
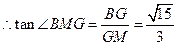
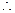 面角
面角 的正切值
的正切值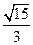 ………………………………………………12分
………………………………………………12分
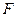 为
为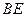 的中点时,
的中点时,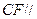 平面
平面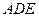 ………………………………1分
………………………………1分证明:取
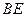 的中点
的中点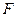 、
、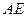 的中点
的中点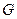 ,连结
,连结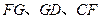

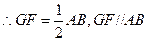
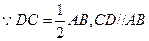 B
B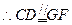
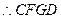 是平行四边形……………………3分
是平行四边形……………………3分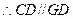
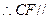 平面
平面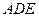 …………………………4分
…………………………4分(Ⅱ)
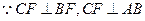
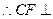 平面
平面
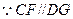
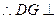 平面
平面 ……………………………………………………………………6分
……………………………………………………………………6分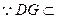 平面
平面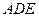
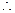 平面
平面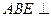 平面
平面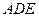 ……………………………………………………………7分
……………………………………………………………7分(Ⅲ)
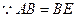
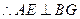
 平面
平面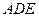
过
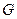 作
作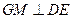 ,连结
,连结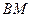 ,则
,则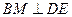
则
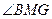 为二面角
为二面角 的平面角………………………………………9分
的平面角………………………………………9分设
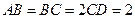 ,则
,则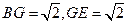
在
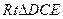 中,
中,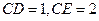
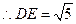
又
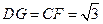
由
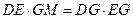 得
得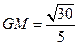 …………………………………………11分
…………………………………………11分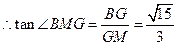
 面角
面角 的正切值
的正切值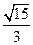 ………………………………………………12分
………………………………………………12分
练习册系列答案
相关题目
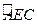 是半径为
是半径为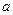 的半圆,
的半圆,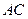 为直径,点
为直径,点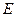 为
为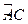 的中点,点
的中点,点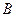 和点
和点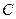 为线段
为线段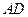 的三等分点,平面
的三等分点,平面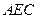 外一点
外一点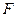 满足
满足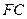
 平面
平面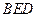 ,
,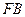 =
=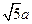 .
. 
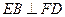 ;
; 的距离.
的距离.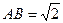 ,
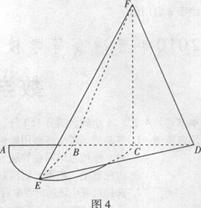
,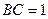 ,现沿对角线
,现沿对角线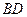 折成二面角
折成二面角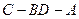 ,使
,使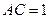 (如图).
(如图).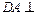 面
面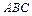 ;
;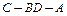 平面角的大小.
平面角的大小.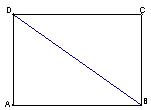

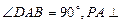 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=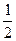 AB=1,M是PB的中点。
AB=1,M是PB的中点。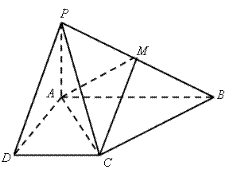
 ,
,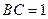 ,设AE与平面ABC所成的角为
,设AE与平面ABC所成的角为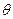 ,且
,且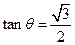 ,
,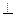 平面ABC.
平面ABC.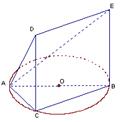
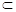 α,则l∥β
α,则l∥β 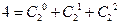 ,
,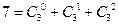 ,
,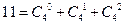 ;……
;……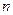 条直线将一个平面最多分成多少个部分(
条直线将一个平面最多分成多少个部分(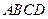 的顶点
的顶点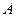 ,
,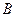 ,
,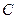 分别在两两垂直的三条射线
分别在两两垂直的三条射线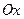 ,
,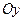 ,
,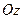 上,则在下列命题中,正确命题的个数为_______.
上,则在下列命题中,正确命题的个数为_______.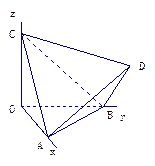
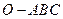 是正三棱锥 ;
是正三棱锥 ;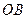 ∥平面
∥平面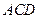 ;
;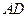 与
与 ;
;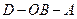 为
为