Question

【题目】设等比数列的公比为，前项和.

（1）求的取值范围；

（2）设，记的前项和为，试比较与的大小.

Answer 1

【答案】（1）；

（2）或时， ； 或时， ； ，或时， .

【解析】试题分析：

（1）由可得，根据等比数列前n项和公式，当时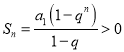， ，分析分子分母同号异号的不同情况，解出的取值范围，当时， 成立；（2）把的通项公式代入，可得和的关系，进而可知和的关系，再根据（1）中的得范围来判断与的大小.

试题解析：

（1）因为是等比数列， 可得.

当时， ，

当时， ，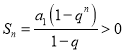

即

上式等价于不等式组： ①

或②

解①式得；解②，由于可为奇数、可为偶数，得.

综上， 的取值范围是.

（2）由得

， .

于是.

又因为，且或，所以，

当或时， ，即；

当或时， ，即；

当，或时， ，即.