ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ρ≥ –ΉΦ±Η‘ΎΒά¬ΖEFΒΡ“Μ≤ύ–όΫ®“ΜΧθ‘ΥΕ·±»»ϋΒάΘ§»ϋΒάΒΡ«Α“Μ≤ΩΖ÷ΈΣ«ζœΏΕΈFBCΘ§ΗΟ«ζœΏΕΈ «Κ· ΐ ![]() Θ®AΘΨ0Θ§ΠΊΘΨ0Θ©Θ§xΓ [©¹4Θ§0] ±ΒΡΆΦœσΘ§«“ΆΦœσΒΡΉνΗΏΒψΈΣBΘ®©¹1Θ§2Θ©Θ°»ϋΒάΒΡ÷–Φδ≤ΩΖ÷ΈΣ≥Λ
Θ®AΘΨ0Θ§ΠΊΘΨ0Θ©Θ§xΓ [©¹4Θ§0] ±ΒΡΆΦœσΘ§«“ΆΦœσΒΡΉνΗΏΒψΈΣBΘ®©¹1Θ§2Θ©Θ°»ϋΒάΒΡ÷–Φδ≤ΩΖ÷ΈΣ≥Λ ![]() «ßΟΉΒΡ÷±œΏ≈ήΒάCDΘ§«“CDΓΈEFΘ°»ϋΒάΒΡΚσ“Μ≤ΩΖ÷ «“‘OΈΣ‘≤–ΡΒΡ“ΜΕΈ‘≤ΜΓ
«ßΟΉΒΡ÷±œΏ≈ήΒάCDΘ§«“CDΓΈEFΘ°»ϋΒάΒΡΚσ“Μ≤ΩΖ÷ «“‘OΈΣ‘≤–ΡΒΡ“ΜΕΈ‘≤ΜΓ ![]() Θ°
Θ° 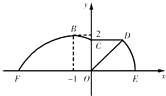
Θ®1Θ©«σΠΊΒΡ÷ΒΚΆΓœDOEΒΡ¥σ–ΓΘΜ
Θ®2Θ©»τ“Σ‘Ύ‘≤ΜΓ»ϋΒάΥυΕ‘”ΠΒΡ…»–ΈODE«χ”ρΡΎΫ®“ΜΗωΓΑΨΊ–Έ≤ίΤΚΓ±Θ§ΨΊ–ΈΒΡ“Μ±Ώ‘ΎΒά¬ΖEF…œΘ§“ΜΗωΕΞΒψ‘ΎΑκΨΕOD…œΘ§ΝμΆβ“ΜΗωΕΞΒψP‘Ύ‘≤ΜΓ ![]() …œΘ§«“ΓœPOE=Π»Θ§«σΒ±ΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐ»ΓΉν¥σ÷Β ±Π»ΒΡ÷ΒΘ°
…œΘ§«“ΓœPOE=Π»Θ§«σΒ±ΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐ»ΓΉν¥σ÷Β ±Π»ΒΡ÷ΒΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚ”…ΧθΦΰΘ§ΒΟA=2Θ§ ![]() Θ°
Θ°
ΓΏ ![]() Θ§Γύ
Θ§Γύ ![]() Θ°
Θ°
Γύ«ζœΏΕΈFBCΒΡΫβΈω ΫΈΣ ![]() Θ°
Θ°
Β±x=0 ±Θ§ ![]() Θ°”÷CD=
Θ°”÷CD= ![]() Θ§Γύ
Θ§Γύ ![]() Θ°
Θ°
Θ®2Θ©ΫβΘΚ”…Θ®1Θ©Θ§Ω…÷Σ ![]() Θ°
Θ°
”÷“Ή÷ΣΒ±ΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐΉν¥σ ±Θ§ΒψP‘ΎΜΓDE…œΘ§Ι ![]() Θ°
Θ°
…ηΓœPOE=Π»Θ§ ![]() Θ§ΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐΈΣ
Θ§ΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐΈΣ ![]()
= ![]() Θ°
Θ°
ΓΏ ![]() Θ§Ι
Θ§Ι ![]() »ΓΒΟΉν¥σ÷Β
»ΓΒΟΉν¥σ÷Β
ΓΨΫβΈωΓΩΘ®1Θ©“άΧβ“βΘ§ΒΟA=2Θ§ ![]() Θ°ΗυΨί÷ήΤΎΙΪ ΫT=
Θ°ΗυΨί÷ήΤΎΙΪ ΫT= ![]() Ω…ΒΟΠΊΘ§Α―BΒΡΉχ±ξ¥ζ»κΫαΚœ“―÷ΣΩ…ΒΟΠ’Θ§¥”ΕχΩ…«σΓœDOEΒΡ¥σ–ΓΘΜΘ®2Θ©”…Θ®1Θ©Ω…÷ΣOD=OPΘ§ΨΊ–Έ≤ίΤΚΒΡΟφΜΐSΙΊ”ΎΠ»ΒΡΚ· ΐΘ§”–
Ω…ΒΟΠΊΘ§Α―BΒΡΉχ±ξ¥ζ»κΫαΚœ“―÷ΣΩ…ΒΟΠ’Θ§¥”ΕχΩ…«σΓœDOEΒΡ¥σ–ΓΘΜΘ®2Θ©”…Θ®1Θ©Ω…÷ΣOD=OPΘ§ΨΊ–Έ≤ίΤΚΒΡΟφΜΐSΙΊ”ΎΠ»ΒΡΚ· ΐΘ§”– ![]() Θ§ΫαΚœ’ΐœ“Κ· ΐΒΡ–‘÷ Ω…«σS»ΓΒΟΉν¥σ÷ΒΘ°
Θ§ΫαΚœ’ΐœ“Κ· ΐΒΡ–‘÷ Ω…«σS»ΓΒΟΉν¥σ÷ΒΘ°
ΓΨΩΦΒψΨΪΈωΓΩ»œ’φ…σΧβΘ§ Ήœ»–η“ΣΝΥΫβ»ΐΫ«Κ· ΐΒΡΉν÷Β(Κ· ΐ![]() Θ§Β±
Θ§Β±![]() ±Θ§»ΓΒΟΉν–Γ÷ΒΈΣ
±Θ§»ΓΒΟΉν–Γ÷ΒΈΣ![]() ΘΜΒ±
ΘΜΒ±![]() ±Θ§»ΓΒΟΉν¥σ÷ΒΈΣ
±Θ§»ΓΒΟΉν¥σ÷ΒΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() Θ§
Θ§![]() )Θ°
)Θ°

 ΩΈΧΟ»ΪΫβΉ÷¥ ΨδΕΈΤΣ’¬œΒΝ–¥πΑΗ
ΩΈΧΟ»ΪΫβΉ÷¥ ΨδΕΈΤΣ’¬œΒΝ–¥πΑΗ ≤Ϋ≤ΫΗΏΩΎΥψΧβΩ®œΒΝ–¥πΑΗ
≤Ϋ≤ΫΗΏΩΎΥψΧβΩ®œΒΝ–¥πΑΗ ΒψΨΠ–¬ΫΧ≤Ρ»ΪΡήΫβΕΝœΒΝ–¥πΑΗ
ΒψΨΠ–¬ΫΧ≤Ρ»ΪΡήΫβΕΝœΒΝ–¥πΑΗ