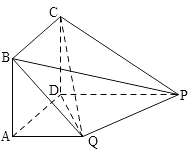
题目内容
【题目】设f（x）=ax2+（a﹣2）x﹣2（a∈R）．
（1）解关于x的不等式f（x）≥0；
（2）若a＞0，当﹣1≤x≤1时，f（x）≤0时恒成立，求a的取值范围．
（3）若当﹣1＜a＜1时，f（x）＞0时恒成立，求x的取值范围．
【答案】
（1）解：由不等式f（x）≥0可得，（ax﹣2）（x+1）≥0．
当a=0时，不等式可化为﹣2（x+1）≥0，解得x≤﹣1；
当a≠0时，方程（ax﹣2）（x+1）=0有两根 
．
若a＜﹣2， 
，由（ax﹣2）（x+1）≥0，解得 
；
若a=﹣2，不等式可化为﹣2（x+1）2≥0，解得x=﹣1；
若﹣2＜a＜0， 
，由（ax﹣2）（x+1）≥0，解得 
；
若a＞0， 
，由（ax﹣2）（x+1）≥0，解得 
；
综上所述，当a=0时，不等式的解集为{x|x≤﹣1}；当a＜﹣2时，不等式的解集为 
；当a=﹣2时，不等式的解集为{﹣1}；当﹣2＜a＜0时，不等式的解集为 
；当a＞0时，不等式的解集为 
．
（2）解：因a＞0，f（x）≤0故函数f（x）开口向上，根据二次函数的特征，若要﹣1≤x≤1时，f（x）≤0时恒成立，只需 
即可．
因此，由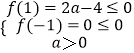 
，
解得0＜a≤2．
所以，a的取值范围为（0，2]．
（3）解：若当﹣1＜a＜1时，设g（a）=a（x2+x）﹣2（x+1）
因此，当﹣1＜a＜1时，f（x）＞0时恒成立等价于当﹣1＜a＜1时，g（a）＞0恒成立．
当x=0时，g（a）=﹣2＜0，不符合题意；
当x=﹣1时，g（a）=0，不符合题意；
当x≠0，x≠﹣1时，只需 
成立即可
即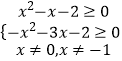 
，解得﹣2≤x≤﹣1．
所以，x的取值范围为[﹣2，﹣1）
【解析】（I）根据a=0和a≠0以及根的大小讨论求解．（II）a＞0，当﹣1≤x≤1时，利用二次方程根的分布，可求a的取值范围．（III）当﹣1＜a＜1时，设g（a）=a（x2+x）﹣2（x+1），g（a）＞0恒成立．看成关于a的一次函数求x的取值范围．
阅读快车系列答案
【题目】某研究所计划利用宇宙飞船进行新产品搭载试验，计划搭载若干件新产品A，B，该研究所要根据产品的研制成本、产品重量、搭载试验费用和预计收益来决定具体安排，通过调查得到的有关数据如表：
每件A产品 | 每件B产品 | |
研制成本、搭载试验费用之和（万元） | 20 | 30 |
产品重量（千克） | 10 | 5 |
预计收益（万元） | 80 | 60 |
已知研制成本、搭载试验费用之和的最大资金为300万元，最大搭载重量为110千克，则如何安排这两种产品进行搭载，才能使总预计收益达到最大，求最大预计收益是 ．
