题目内容
【题目】已知三棱柱ABC﹣A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E、F分别在棱AA′,CC′上,且AE=C′F=2. 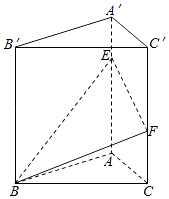
(1)求证:BB′⊥底面ABC;
(2)在棱A′B′上是否存在一点M,使得C′M∥平面BEF,若存在,求 ![]() 值,若不存在,说明理由;
值,若不存在,说明理由;
(3)求棱锥A′﹣BEF的体积.
【答案】
(1)证明:取BC中点O,连接AO,因为三角形ABC是等边三角形,所以AO⊥BC,
又因为平面BCC′B′⊥底面ABC,AO平面ABC,平面BCC′B′∩平面ABC=BC,
所以AO⊥平面BCC′B′,
又BB′平面BCC′B,所以AO⊥BB′.
又BB′⊥AC,AO∩AC=A,AO平面ABC,AC平面ABC.
所以BB′⊥底面ABC
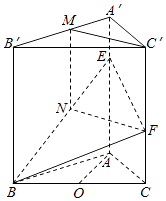
(2)解:显然M不是A′,B′,棱A′B′上若存在一点M,使得C′M∥平面BEF,
过M作MN∥AA′交BE于N,连接FN,MC′,所以MN∥CF,即C′M和FN共面,
所以C′M∥FN,
所以四边形C′MNF为平行四边形,所以MN=2,
所以MN是梯形A′B′BE的中位线,M为A′B′的中点.即 ![]()
(3)解: ![]()
【解析】(1)取BC中点O,先证AO⊥BC,再由面面垂直的性质定理证得AO⊥面BCC'B',再由线面垂直的判定定理即可得证;(2)显然M不是A′,B′,棱A′B′上若存在一点M,使得C′M∥平面BEF,可通过线面平行的判断定理,即可证得;(3)利用等体积转化,即可求棱锥A′﹣BEF的体积.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 名题金卷系列答案
名题金卷系列答案【题目】某研究所计划利用宇宙飞船进行新产品搭载试验,计划搭载若干件新产品A,B,该研究所要根据产品的研制成本、产品重量、搭载试验费用和预计收益来决定具体安排,通过调查得到的有关数据如表:
每件A产品 | 每件B产品 | |
研制成本、搭载试验费用之和(万元) | 20 | 30 |
产品重量(千克) | 10 | 5 |
预计收益(万元) | 80 | 60 |
已知研制成本、搭载试验费用之和的最大资金为300万元,最大搭载重量为110千克,则如何安排这两种产品进行搭载,才能使总预计收益达到最大,求最大预计收益是 .