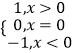题目内容
【题目】如图,定义在[﹣1,5]上的函数f(x)由一段线段和抛物线的一部分组成. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)指出函数f(x)的自变量x在什么范围内取值时,函数值大于0,小于0或等于0(不需说理由).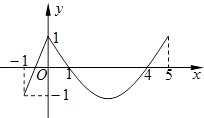
【答案】解:(Ⅰ)当﹣1≤x≤0时,直线过点(0,1)和(﹣1,﹣1),则对应的直线方程为f(x)=kx+1, ∵f(﹣1)=﹣k+1=﹣1,
∴k=2,即f(x)=2x+1,
当0≤x≤5时,抛物线与x轴的交点为(1,0)和(4,0),
∴设f(x)=a(x﹣1)(x﹣4),
∵f(0)=4a=1,
∴a= ![]() ,
,
即f(x)= ![]() (x﹣1)(x﹣4),0≤x≤5.
(x﹣1)(x﹣4),0≤x≤5.
(Ⅱ)由f(x)=2x+1=0,得x=﹣ ![]() ,
,
∴当﹣ ![]() <x<1或4<x<5时,函数值大于0,
<x<1或4<x<5时,函数值大于0,
当﹣1<x<﹣ ![]() 或1<x<4时,函数值小于0,
或1<x<4时,函数值小于0,
当x=﹣ ![]() 或x=1或x=45时,函数值等于0
或x=1或x=45时,函数值等于0
【解析】(Ⅰ)利用待定系数法求函数f(x)的解析式;(Ⅱ)根据函数的图象确定函数值对应的取值范围.

练习册系列答案
相关题目