Question

【题目】如图，△ABC是边长为4的等边三角形，△ABD是等腰直角三角形，AD⊥BD，平面ABC⊥平面ABD，且EC⊥平面ABC，EC=2．

（1）求证：AD⊥BE
（2）求平面AEC和平面BDE所成锐二面角的余弦值．

Answer 1

【答案】
（1）解：以OA，OC，OD为x，y，z的正方向建立直角坐标系，

则有：

由于 ，

故AD⊥BE．

（2）解：如图建立坐标系，

则 ，

，

设平面AEC的法向量为 ，

则 所以 ，

令y1=1，则

所以 ，

设平面BDE的法向量为

则 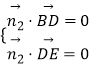所以 ，令x2=1，则y2=0，z1=﹣1

所以 ，

所以 ．

【解析】（1）建立空间坐标系，求出点的坐标，利用向量法证明直线垂直．（2）求出平面的法向量，利用向量法进行求解即可．
【考点精析】根据题目的已知条件，利用空间中直线与直线之间的位置关系的相关知识可以得到问题的答案，需要掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点．