题目内容
【题目】设数列{an}的前n项和为Sn,且Sn=4an﹣p,其中p是不为零的常数.
(1)证明:数列{an}是等比数列;
(2)当p=3时,若数列{bn}满足bn+1=bn+an(n∈N*),b1=2,求数列{bn}的通项公式.
【答案】(1)见解析;
(2)见解析.
【解析】
试题分析:(1)通过Sn=4an﹣p,利用an=Sn﹣Sn﹣1,求出![]() ,利用等比数列的定义证明数列{an}是等比数列;
,利用等比数列的定义证明数列{an}是等比数列;
(2)当p=3时,若数列{bn}满足bn+1=bn+an(n∈N*),b1=2,推出![]() ,利用bn=b1+(b2﹣b′1)+(b3﹣b2)++(bn﹣bn﹣1),求数列{bn}的通项公式.
,利用bn=b1+(b2﹣b′1)+(b3﹣b2)++(bn﹣bn﹣1),求数列{bn}的通项公式.
证明:(1)证:因为Sn=4an﹣p(n∈N*),则Sn﹣1=4an﹣1﹣p(n∈N*,n≥2),
所以当n≥2时,an=Sn﹣Sn﹣1=4an﹣4an﹣1,整理得![]() .
.
由Sn=4an﹣p,令n=1,得a1=4a1﹣p,解得![]() .
.
所以an是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
(2)解:因为a1=1,则![]() ,
,
由bn+1=an+bn(n=1,2,),得![]() ,
,
当n≥2时,由累加得bn=b1+(b2﹣b′1)+(b3﹣b2)+…+(bn﹣bn﹣1)=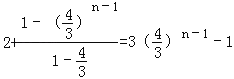 ,
,
当n=1时,上式也成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】根据以往的经验,某工程施工期间的将数量X(单位:mm)对工期的影响如下表:
降水量X | X<300 | 300≤X<700 | 700≤X<900 | X≥900 |
工期延误天数Y | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9,求:
(I)工期延误天数Y的均值与方差;
(Ⅱ)在降水量X至少是300的条件下,工期延误不超过6天的概率.

