Question

【题目】在平面直角坐标系xOy中，直线l的参数方程为 （t为参数），在以坐标原点O为极点，x轴的正非负半轴为极轴，取相同单位长度的极坐标系中，圆的极坐标方程为ρ=4sinθ．
（1）求直线l被圆截得的弦长；
（2）从极点作圆C的弦，求各弦中点的极坐标方程．

Answer 1

【答案】
（1）解：依题，把直线l的参数方程化为普通方程为y= x，

把圆C的极坐标方程化为直角坐标方程为x2+y2=4y，即x2+（y﹣2）2=4，…（3分）

则点C（0，2）到直线l的距离d= ，于是所求的弦长为 ；

（2）解：记所作的弦为OA，设A（ρ0，θ0），弦OA的中点M（ρ，θ），

则 ，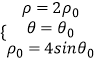

消去ρ0，θ0，可得ρ=2sinθ即中点的极坐标方程．

【解析】（1）求出直线的普通方程，以及圆的普通方程，利用圆心到直线的距离以及半径半弦长的关系，求直线l被圆截得的弦长；（2）从极点作圆C的弦，设A（ρ0 ， θ0），弦OA的中点M（ρ，θ），列出关系式，即可求各弦中点的极坐标方程．