题目内容
18.已知数列{an}和{bn}满足a1•a2•a3…an=($\sqrt{2}$)${\;}^{{b}_{n}}$(n∈N*).若{an}是各项均为正数的等比数列,且a1=2,b3=6+b2,求bn=n(n+1).分析 由已知式子易得等比数列{an}的公比q=2,进而由已知等式和指数的运算可得.
解答 解:设等比数列{an}的公比为q,
∵a1•a2•a3…an=($\sqrt{2}$)${\;}^{{b}_{n}}$(n∈N*).,
∴a1•a2•a3=$(\sqrt{2})^{{b}_{3}}$,∴a13q3=8q3=$(\sqrt{2})^{{b}_{3}}$,
同理可得a1•a2=$(\sqrt{2})^{{b}_{2}}$,∴a12q=4q=$(\sqrt{2})^{{b}_{2}}$,
又b3=6+b2,∴8q3=$(\sqrt{2})^{6+{b}_{2}}$=$(\sqrt{2})^{6}$×$(\sqrt{2})^{{b}_{2}}$=8×4q,
解得q=2或q=-2,
∵a1•a2=$(\sqrt{2})^{{b}_{2}}$>0,∴q=2,
∴an=a1qn-1=2n,又a1•a2•a3…an=($\sqrt{2}$)${\;}^{{b}_{n}}$(n∈N*),
∴2n•${2}^{\frac{n(n-1)}{2}}$=${2}^{\frac{{b}_{n}}{2}}$,∴bn=n(n+1),
故答案为:n(n+1)
点评 本题考查等比数列的通项公式,涉及分类讨论和指数的运算,属中档题.

练习册系列答案
相关题目
9.已知f(x)=3sinx-πx,对任意的x∈(0,$\frac{π}{2}$),给出以下四个结论:
①f′(x)>0;
②f′(x)<0;
③f(x)>0;
④f(x)<0.
其中正确的是( )
①f′(x)>0;
②f′(x)<0;
③f(x)>0;
④f(x)<0.
其中正确的是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
6.已知a、b、c分别为△ABC三个内角A,B,C的对边,若A=$\frac{π}{3}$,则a(cosC+$\sqrt{3}$sinC)=( )
| A. | a+b | B. | b+c | C. | a+c | D. | a+b+c |
13.执行如图所示的程序框图,则输出结果S=( )
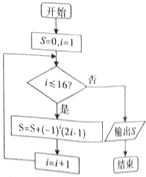

| A. | 14 | B. | 16 | C. | 19 | D. | 21 |
3.设全集U=R,A={x||x|<2},B={x|y=$\sqrt{x-1}$},则图中阴影部分所表示的集合( )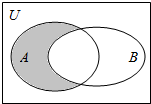

| A. | (-2,+∞) | B. | (1,2] | C. | (-2,1) | D. | (-2,1] |
8.运行如图所示的程序框图,若输出的结果是36,则输入的n=( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |