题目内容
已知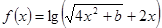 ,其中
,其中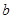 是常数.
是常数.
(1))当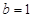 时,
时, 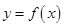 是奇函数;
是奇函数;
(2)当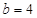 时,
时,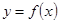 的图像上不存在两点
的图像上不存在两点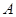 、
、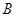 ,使得直线
,使得直线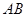 平行于
平行于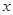 轴.
轴.
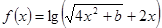 ,其中
,其中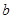 是常数.
是常数.(1))当
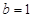 时,
时, 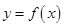 是奇函数;
是奇函数;(2)当
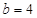 时,
时,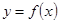 的图像上不存在两点
的图像上不存在两点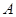 、
、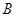 ,使得直线
,使得直线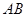 平行于
平行于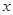 轴.
轴.证明见解析.
试题分析:(1)奇函数的问题,可以根据奇函数的定义,利用
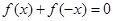 来解决,当然如果你代数式变形的能力较强,可以直接求
来解决,当然如果你代数式变形的能力较强,可以直接求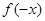 然后化简变形为
然后化简变形为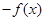 ,从而获得证明;(2)要证明函数
,从而获得证明;(2)要证明函数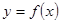 的图像上不存在两点A、B,使得直线AB平行于
的图像上不存在两点A、B,使得直线AB平行于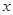 轴,即方程
轴,即方程 不可能有两个或以上的解,最多只有一个解,
不可能有两个或以上的解,最多只有一个解,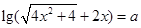
 ,
,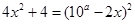
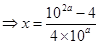 ,因此原方程最多只有一解,或者用反证法证明,设存在,即有两个
,因此原方程最多只有一解,或者用反证法证明,设存在,即有两个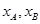 ,且
,且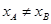 ,使
,使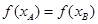 ,然后推理得到矛盾的结论,从而完成证明.
,然后推理得到矛盾的结论,从而完成证明.试题解析:(1)由题意,函数定义域
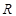 , 1分
, 1分对定义域任意
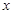 ,有:
,有: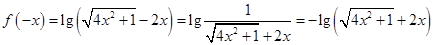 4分
4分所以
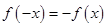 ,即
,即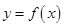 是奇函数. 6分
是奇函数. 6分(2)假设存在不同的
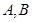 两点,使得
两点,使得 平行
平行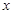 轴,则
轴,则 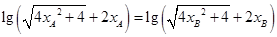 9分
9分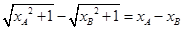
化简得:
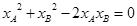 ,即
,即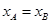 ,与
,与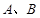 不同矛盾。 13分
不同矛盾。 13分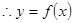 的图像上不存在两点,使得所连的直线与
的图像上不存在两点,使得所连的直线与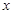 轴平行 14分
轴平行 14分
练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
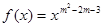 (
(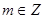 )在
)在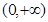 是单调减函数,且为偶函数.
是单调减函数,且为偶函数.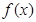 的解析式;
的解析式; 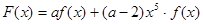 的奇偶性,并说明理由.
的奇偶性,并说明理由.
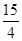
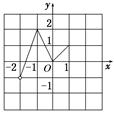
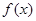 是定义在
是定义在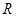 上的奇函数,满足
上的奇函数,满足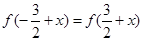 ,当
,当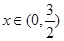 时,
时,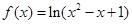 ,则函数
,则函数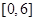 上的零点个数是( )
上的零点个数是( ) 
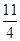
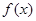 为
为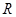 上的偶函数,且对任意
上的偶函数,且对任意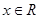 均有
均有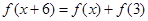 成立且
成立且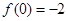 ,当
,当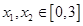 且
且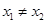 时,有
时,有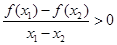 ,给出四个命题:
,给出四个命题: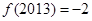 ;
;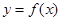 的图像关于
的图像关于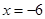 对称;
对称;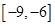 上为增函数;
上为增函数;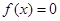 在
在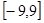 上有4个实根.
上有4个实根.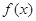 的定义域为R,
的定义域为R,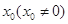 是
是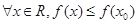
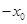 是
是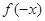 的极小值点
的极小值点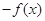 的极小值点
的极小值点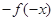 的极小值点
的极小值点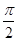 的奇函数
的奇函数