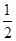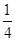题目内容
已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax-a-x+2(a>0且a≠1),若g(2)=a,则f(2)等于( )
| A.2 | B. |
C.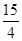 | D.a2 |
C
由题意得
f(-x)+g(-x)=g(x)-f(x)=a-x-ax+2,
联立f(x)+g(x)=ax-a-x+2,
求解得g(x)=2,f(x)=ax-a-x.
故a=2,f(2)=22-2-2=4-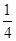 =
=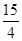 .故选C.
.故选C.
f(-x)+g(-x)=g(x)-f(x)=a-x-ax+2,
联立f(x)+g(x)=ax-a-x+2,
求解得g(x)=2,f(x)=ax-a-x.
故a=2,f(2)=22-2-2=4-
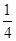 =
=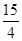 .故选C.
.故选C.
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
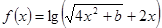 ,其中
,其中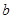 是常数.
是常数.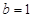 时,
时, 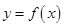 是奇函数;
是奇函数;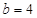 时,
时,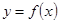 的图像上不存在两点
的图像上不存在两点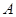 、
、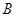 ,使得直线
,使得直线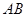 平行于
平行于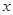 轴.
轴.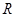 上的偶函数
上的偶函数 满足
满足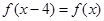 ,且在区间[0,2]上
,且在区间[0,2]上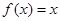 ,若关于
,若关于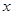 的方程
的方程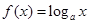 有三个不同的根,则
有三个不同的根,则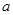 的范围为( )
的范围为( )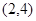
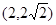
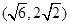

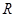 上的函数
上的函数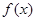 满足
满足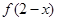 为奇函数,函数
为奇函数,函数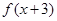 关于直线
关于直线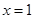 对称,则下列式子一定成立的是( )
对称,则下列式子一定成立的是( )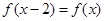
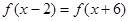

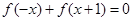
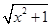
 )+f(1)+f(
)+f(1)+f( )+f(2)+f(
)+f(2)+f( )
)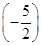 等于( )
等于( )