题目内容
3．若定义在R上的函数f（x）满足f（x+2）=f（x），且当x∈（-1，1]时，f（x）=x，则函数$y=f（x）-{log_{\frac{1}{3}}}$|x|的零点个数是（ ）| A． | 0 | B． | 2 | C． | 4 | D． | 8 |
分析 根据函数周期性的概念，奇偶性，作出图象，再利用两个图象求出交点个数
解答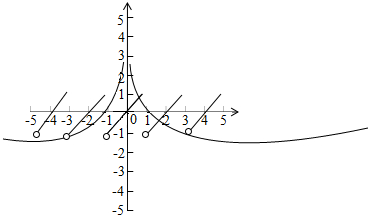 
解：∵在R上的函数y=f（x）满足f（x+2）=f（x），∴函数y=f（x）的周期T=2，
∵当x∈（-1，1]时，f（x）=x，
∵g（x）=log${\;}_{\frac{1}{3}}$|x|是偶函数，在（0，+∞）单调递减，在（-∞，0）上单调递增，
∴g（-1）=g（1）=0，g（-3）=g（3）=-1，f（1）=1
∴y轴右侧2个交点，y轴左侧没有交点，
故选：B．
点评 本题考查了函数的奇偶性，周期性，在图象中的应用，运用数形结合思想解决
练习册系列答案
阅读快车系列答案
相关题目
14．设数列是{an}（n∈N*）是等差数列，若a1+a5=4，则a3=（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 4 |
18．若集合A={（x，y）||x-1|+$\sqrt{y-4}$=0}，B={1，4}，则下面选项正确的是（ ）
| A． | B⊆A | B． | A⊆B | C． | A=B | D． | A∩B=Φ |
15．
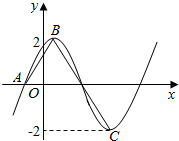已知函数$f（x）=2sin（ωx+φ）（ω＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示，A、B、C分别是函数图象与x轴交点、图象的最高点、图象的最低点．若f（0）=$\sqrt{3}$，
且$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{π}^{2}}{8}$-8．则f（x）的解析式为（ ）
已知函数$f（x）=2sin（ωx+φ）（ω＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示，A、B、C分别是函数图象与x轴交点、图象的最高点、图象的最低点．若f（0）=$\sqrt{3}$，且$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{π}^{2}}{8}$-8．则f（x）的解析式为（ ）
| A． | f（x）=2sin（2x+$\frac{π}{3}$） | B． | f（x）=2sin（2x+$\frac{π}{6}$） | C． | f（x）=2sin（3x+$\frac{π}{3}$） | D． | f（x）=2sin（3x+$\frac{π}{6}$） |