题目内容
13.已知函数f(x)定义域为R,对任意的x∈R都有f(x)=f(x+2),且当-1<x<0时,f(x)=($\frac{1}{2}$)x-1,当0≤x≤1时,f(x)=x,则函数g(x)=f(x)-log5x的零点个数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 函数g(x)=f(x)-log5x的零点个数可化为函数f(x)与函数y=log5x的交点的个数;作出图象求解即可.
解答 解:函数g(x)=f(x)-log5x的零点个数可化为
函数f(x)与函数y=log5x的交点的个数;
作函数f(x)与函数y=log5x的图象如下,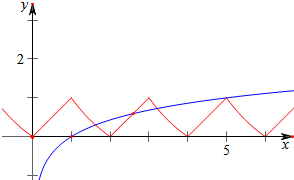
结合图象可知,
函数f(x)与函数y=log5x有四个不同的交点,
故函数g(x)=f(x)-log5x的零点个数为4;
故选:B.
点评 本题考查了函数图象的作法及数形结合的思想应用,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
3.函数值tan224°,sin136°,cos310°的大小关系是( )
| A. | cos310°<sin136°<tan224° | B. | sin136°<cos310°<tan224° | ||
| C. | cos310°<tan224°<sin136° | D. | tan224°<sin136°<cos310° |
4.对于R上可导的任意函数f(x),若满足(x-2)f′(x)≥0,则必有( )
| A. | f(0)+f(3)<2f(2) | B. | f(0)+f(3)≤2f(2) | C. | f(0)+f(3)≥2f(2) | D. | f(0)+f(3)>2f(2) |
18.圆:x2+y2-4x+6y=0的圆心坐标和半径分别为( )
| A. | (-2,3),13 | B. | (-2,3),$\sqrt{13}$ | C. | (2,-3),$\sqrt{13}$ | D. | (2,-3),13 |
2.已知直线x-2y+n=0与圆O:x2+y2=4交于A,B两点,若∠AOB=60°,则实数n的值为( )
| A. | $\sqrt{15}$ | B. | $2\sqrt{15}$ | C. | $±\sqrt{15}$ | D. | $±2\sqrt{15}$ |
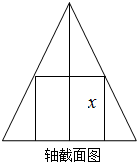 一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱:
一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱: