题目内容
8.已知函数f(x)=2x3+3x2+1(x∈R).(1)求函数f(x)的图象在点A(1,6)处的切线方程;
(2)求f(x)的单调区间.
分析 (1)求得函数的导数,确定切线的斜率和切点坐标,运用点斜式方程即可得到切线方程;
(2)求得导数,令导数大于0,可得增区间,令导数小于0,可得减区间.
解答 解:(1)因为f'(x)=6x2+6x,…(2分)
所以f'(1)=12,…(4分)
函数f(x)的图象在点(1,6)处的切线方程为:y-6=12(x-1)…(5分)
即:y=12x-6…(6分)
(2)f'(x)=6x2+6x=6x(x+1)…(7分)
令f′(x)>0,则x>0或x<-1…(9分)令f′(x)<0,则-1<x<0…(11分)
∴f(x)的增区间为(0,+∞),(-∞,-1)减区间为(-1,0)…(12分)
点评 本题考查导数的运用:求切线方程和单调区间,正确求导和运用对数函数的单调性是解题的关键.

练习册系列答案
相关题目
18.圆:x2+y2-4x+6y=0的圆心坐标和半径分别为( )
| A. | (-2,3),13 | B. | (-2,3),$\sqrt{13}$ | C. | (2,-3),$\sqrt{13}$ | D. | (2,-3),13 |
3.若定义在R上的函数f(x)满足f(x+2)=f(x),且当x∈(-1,1]时,f(x)=x,则函数$y=f(x)-{log_{\frac{1}{3}}}$|x|的零点个数是( )
| A. | 0 | B. | 2 | C. | 4 | D. | 8 |
13.如果cosα=$\frac{4}{5}$,那么$sin(α+\frac{π}{4})-\frac{{\sqrt{2}}}{2}$cosα等于( )
| A. | $\frac{{2\sqrt{2}}}{5}$ | B. | ±$\frac{{2\sqrt{2}}}{5}$ | C. | $\frac{{3\sqrt{2}}}{10}$ | D. | ±$\frac{{3\sqrt{2}}}{10}$ |
17.已知cosx=$\frac{1}{3}$,则cos2x=( )
| A. | $\frac{2}{3}$ | B. | -$\frac{8}{9}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
9.${(\root{3}{x}+\frac{1}{x})^n}$的展开式中第5项是常数项,那么这个展开式中系数最大的项为( )
| A. | 第9项 | B. | 第8项 | C. | 第9项和第10项 | D. | 第8项和第9项 |
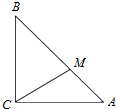 如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,
如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,