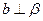题目内容
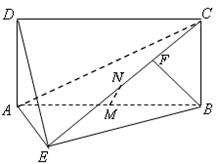
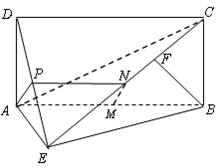
(12分)如图,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,
且BF⊥平面ACE.
(1)求证:AE⊥BE;
(2)设点M为线段AB的中点,点N为线段CE的中点.
求证:MN∥平面DAE.

且BF⊥平面ACE.
(1)求证:AE⊥BE;
(2)设点M为线段AB的中点,点N为线段CE的中点.
求证:MN∥平面DAE.



同解析

证明:(1)∵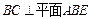 ,
,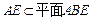 ,∴
,∴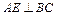 ,
,
又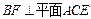 ,
,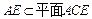 ,∴
,∴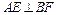 ,…………………………(3分)
,…………………………(3分)
又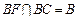 ,∴
,∴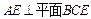 ,又
,又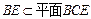 ,
,
∴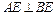 .…………………………(6分)
.…………………………(6分)
(2)取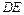 的中点
的中点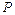 ,连接
,连接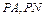 ,
,
∵点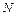 为线段
为线段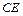 的中点.
的中点.
∴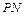 ∥
∥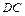 ,且
,且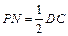 , ……………………(8分)
, ……………………(8分)
又四边形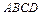 是矩形,点
是矩形,点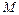 为线段
为线段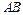 的中点,∴
的中点,∴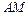 ∥
∥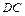 ,且
,且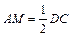 ,
,
∴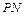 ∥
∥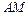 ,且
,且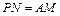 ,故四边形
,故四边形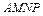 是平行四边形,
是平行四边形,
∴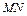 ∥
∥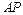 …………(10分)
…………(10分)
而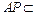 平面
平面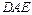 ,
,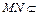 平面
平面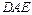 ,∴
,∴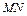 ∥平面
∥平面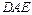 . …………………(12分)
. …………………(12分)
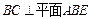 ,
,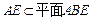 ,∴
,∴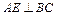 ,
,又
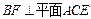 ,
,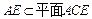 ,∴
,∴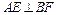 ,…………………………(3分)
,…………………………(3分)又
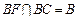 ,∴
,∴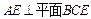 ,又
,又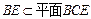 ,
,∴
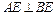 .…………………………(6分)
.…………………………(6分)(2)取
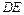 的中点
的中点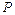 ,连接
,连接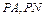 ,
,∵点
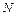 为线段
为线段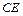 的中点.
的中点.∴
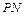 ∥
∥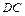 ,且
,且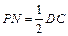 , ……………………(8分)
, ……………………(8分)又四边形
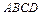 是矩形,点
是矩形,点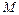 为线段
为线段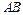 的中点,∴
的中点,∴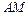 ∥
∥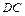 ,且
,且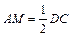 ,
,∴
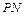 ∥
∥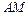 ,且
,且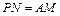 ,故四边形
,故四边形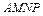 是平行四边形,
是平行四边形,∴
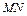 ∥
∥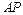 …………(10分)
…………(10分) 而
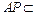 平面
平面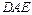 ,
,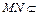 平面
平面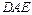 ,∴
,∴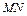 ∥平面
∥平面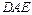 . …………………(12分)
. …………………(12分)
练习册系列答案
相关题目
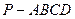 的底面ABCD是正方形,
的底面ABCD是正方形,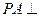 底面ABCD,E,F分别是AC,PB的中点.
底面ABCD,E,F分别是AC,PB的中点.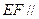 平面PCD;
平面PCD;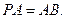 求EF与平面PAC所成角的大小.
求EF与平面PAC所成角的大小.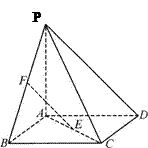
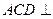 平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在
平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在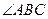 的平分线上。
的平分线上。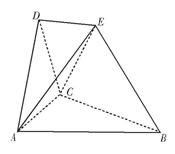
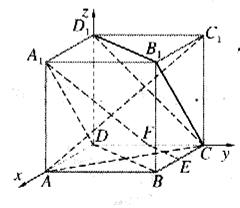
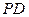 边的中点,且PA⊥底面ABCD。
边的中点,且PA⊥底面ABCD。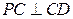

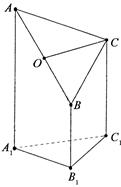
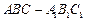 中,已知
中,已知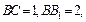
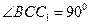 ,
,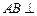 侧面
侧面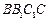
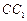 (不包含端点
(不包含端点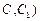 上确定一点
上确定一点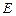 的位置,使得
的位置,使得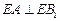 (要求说明理由).
(要求说明理由).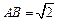 ,求二面角
,求二面角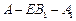 的大小.
的大小.
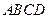 所在平面与平面四边形
所在平面与平面四边形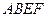 所在平面互相垂直,△
所在平面互相垂直,△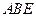 是等腰直角三角形
是等腰直角三角形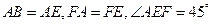
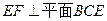 ;
;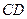 的中点为
的中点为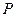 ,在直线
,在直线 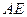 上是否存在一点
上是否存在一点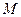 ,使得
,使得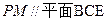 ?若存在,请指出点
?若存在,请指出点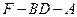 正切值的大小。
正切值的大小。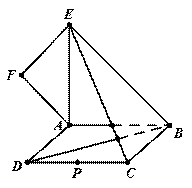
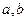 是两条不同的直线,
是两条不同的直线,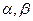 是两个不重合的平面,则下列命题中正确的是
是两个不重合的平面,则下列命题中正确的是 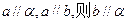
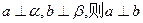
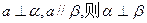
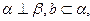 则
则