题目内容
下列命题中是假命题的是( )
| A.?α,β∈R,使sin(α+β)=sinα+sinβ |
B.?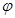 ∈R,函数f(x)=sin(2x+ ∈R,函数f(x)=sin(2x+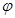 )都不是偶函数 )都不是偶函数 |
C.?m∈R,使f(x)=(m-1)· 是幂函数,且在(0,+∞)上单调递减 是幂函数,且在(0,+∞)上单调递减 |
| D.?a>0,函数f(x)=ln2x+lnx-a有零点 |
B
对于A,β=0时,命题成立,故A为真命题;
对于B,当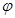 =
=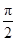 时,f(x)=cos2x是偶函数,∴B为假命题;
时,f(x)=cos2x是偶函数,∴B为假命题;
对于C,若f(x)为幂函数,则m-1=1,∴m=2,此时f(x)=x-1在(0,+∞)上单调递减,故C为真命题;
对于D,f(x)=(lnx+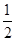 )2-
)2-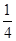 -a,显然?a>0,f(x)=0有解,故D为真命题.故选B.
-a,显然?a>0,f(x)=0有解,故D为真命题.故选B.
对于B,当
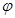 =
=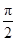 时,f(x)=cos2x是偶函数,∴B为假命题;
时,f(x)=cos2x是偶函数,∴B为假命题;对于C,若f(x)为幂函数,则m-1=1,∴m=2,此时f(x)=x-1在(0,+∞)上单调递减,故C为真命题;
对于D,f(x)=(lnx+
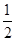 )2-
)2-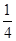 -a,显然?a>0,f(x)=0有解,故D为真命题.故选B.
-a,显然?a>0,f(x)=0有解,故D为真命题.故选B.
练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 x∈[1,2],x2-a≥0,命题q:
x∈[1,2],x2-a≥0,命题q: x0∈R,x+2ax0+2-a=0,若“p且q”为真命题,求实数a的取值范围.
x0∈R,x+2ax0+2-a=0,若“p且q”为真命题,求实数a的取值范围. ,则
,则 或
或 的逆否命题是 .
的逆否命题是 .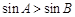 ,则
,则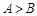 ”的逆命题是真命题;②命题
”的逆命题是真命题;②命题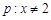 或
或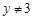 ,命题
,命题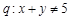 则
则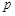 是
是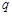 的必要不充分条件;③“
的必要不充分条件;③“ ”的否定是“
”的否定是“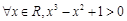 ”;④若随机变量
”;④若随机变量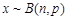 ,则
,则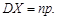 ⑤回归分析中,回归方程可以是非线性方程.
⑤回归分析中,回归方程可以是非线性方程.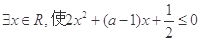 ”是假命题,则实数
”是假命题,则实数 的取值范围是( )
的取值范围是( ) 

 q
q <
< ”及其逆命题、否命题和逆否命题都是假命题,则实数a,b应满足的前提条件是________.
”及其逆命题、否命题和逆否命题都是假命题,则实数a,b应满足的前提条件是________. p:?x∈R,均有x2+x+1≥0
p:?x∈R,均有x2+x+1≥0