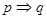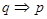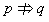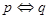题目内容
已知命题p: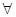 x∈[1,2],x2-a≥0,命题q:
x∈[1,2],x2-a≥0,命题q: x0∈R,x+2ax0+2-a=0,若“p且q”为真命题,求实数a的取值范围.
x0∈R,x+2ax0+2-a=0,若“p且q”为真命题,求实数a的取值范围.
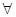 x∈[1,2],x2-a≥0,命题q:
x∈[1,2],x2-a≥0,命题q: x0∈R,x+2ax0+2-a=0,若“p且q”为真命题,求实数a的取值范围.
x0∈R,x+2ax0+2-a=0,若“p且q”为真命题,求实数a的取值范围.a=1或a≤-2
试题分析:求出命题p为真命题的a的范围,再通过分类讨论求出q为真命题的a的范围,“命题p∧q”为真命题,即命题q 命题p都是真命题,写出a的范围..
试题解析:由“p且q”为真命题,则p,q都是真命题.
p:x2≥a在[1,2]上恒成立,只需a≤(x2)min=1,
所以命题p:a≤1; 4分
q:设f(x)=x2+2ax+2-a,存在x0∈R使f(x0)=0,
只需
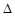 =4a2-4(2-a)≥0,
=4a2-4(2-a)≥0,即a2+a-2≥0⇒a≥1或a≤-2,
所以命题q:a≥1或a≤-2. 8分
由
 得a=1或a≤-2
得a=1或a≤-2故实数a的取值范围是a=1或a≤-2. 12分.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
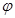 ∈R,函数f(x)=sin(2x+
∈R,函数f(x)=sin(2x+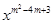 是幂函数,且在(0,+∞)上单调递减
是幂函数,且在(0,+∞)上单调递减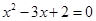 ,则
,则 ”的逆否命题为“若
”的逆否命题为“若 ,则
,则 ”;
”; 中,
中, 增加1个单位时,
增加1个单位时,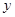 一定增加2个单位;
一定增加2个单位; 为假命题,则
为假命题,则 均为假命题;
均为假命题; ,使得
,使得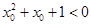 ,则
,则 ,均有
,均有 ;
; ”的否命题为:“若
”的否命题为:“若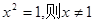 ”.
”.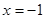 ”是“
”是“ ”的必要不充分条件.
”的必要不充分条件. ”的否定是:“
”的否定是:“ ”.
”. ”的逆否命题为真命题.
”的逆否命题为真命题.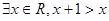

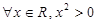

 ,使得
,使得 ”的否定为( )
”的否定为( )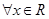 ,都有
,都有
 ”的逆否命题为:“若
”的逆否命题为:“若 ”
” ”的充分不必要条件
”的充分不必要条件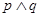 为假命题,则p、q均为假命题
为假命题,则p、q均为假命题
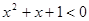 ,则
,则