题目内容
20.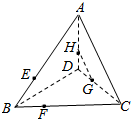 如图,已知点E、F、G、H分别是三棱锥A-BCD棱上的四点,且$\frac{BF}{FC}$=$\frac{BE}{EA}$=$\frac{DH}{HA}$=$\frac{DG}{GC}$=$\frac{1}{2}$.
如图,已知点E、F、G、H分别是三棱锥A-BCD棱上的四点,且$\frac{BF}{FC}$=$\frac{BE}{EA}$=$\frac{DH}{HA}$=$\frac{DG}{GC}$=$\frac{1}{2}$.(1)求证:E、F、G、H四点共面;
(2)若AC⊥BD,求证:四边形EFGH是矩形.
分析 (1)根据题意,证明EF∥GH,即可得出E、F、G、H四点共面;
(2)先证明四边形EFGH是平行四边形,再证明有一角是直角,即可得出四边形EFGH是矩形.
解答 解:(1)证明:点E、F、G、H分别是三棱锥A-BCD棱上的四点,
且$\frac{BF}{FC}$=$\frac{BE}{EA}$=$\frac{DH}{HA}$=$\frac{DG}{GC}$=$\frac{1}{2}$;
∴EF∥AC,GH∥AC,
∴EF∥GH,
∴E、F、G、H四点共面;
(2)证明:如图所示,
∵EH∥BD,FG∥BD,
∴FG∥EH,
又EF∥GH,
∴四边形EFGH是平行四边形,
又AC⊥BD,
∴EF⊥FG,
∴平行四边形EFGH是矩形.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了推理与证明能力的应用问题,是基础题目.

练习册系列答案
相关题目
11.已知数列{an},{bn}满足a1=1,且an,an+1是函数f(x)=x2+bnx+2n的两个零点,则b10=( )
| A. | 32 | B. | -32 | C. | 64 | D. | -64 |
8.若命题P:?x0$>0,{x}_{0}^{2}$+2x0+3≤0,则命题P的否定¬P是( )
| A. | ?x>0,x2+2x+3>0 | B. | ?x>0,x2+2x+3≥0 | C. | ?x≤0,x2+2x+3<0 | D. | ?x≤0,x2+2x+3≤0 |
10.意义运算“*”如下:x*y=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若函数f(x)=(1-2x)*(2x-3)+m的图象与x轴有两个交点,则实数m的取值范围是( )
| A. | (-1,+∞) | B. | (-1,1) | C. | [-1,+∞) | D. | [-1,1) |
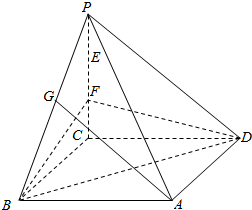 如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,E、F是PC的三等分点,G是PB的中点,过E,A,G三点的平面?FBD是否平行?
如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,E、F是PC的三等分点,G是PB的中点,过E,A,G三点的平面?FBD是否平行?