题目内容
10.已知x${\;}^{\frac{1}{2}}$+x${\;}^{-\frac{1}{2}}$=3,试计算:$\frac{{x}^{2}+{x}^{-2}-7}{x+{x}^{-1}+3}$.分析 利用x${\;}^{\frac{1}{2}}$+x${\;}^{-\frac{1}{2}}$=3,可得x+x-1=$({x}^{\frac{1}{2}}+{x}^{-\frac{1}{2}})^{2}$-2,x2+x-2=(x+x-1)2-2.即可得出.
解答 解:∵x${\;}^{\frac{1}{2}}$+x${\;}^{-\frac{1}{2}}$=3,∴x+x-1=$({x}^{\frac{1}{2}}+{x}^{-\frac{1}{2}})^{2}$-2=32-2=7,
x2+x-2=(x+x-1)2-2=72-2=47.
∴$\frac{{x}^{2}+{x}^{-2}-7}{x+{x}^{-1}+3}$=$\frac{47-7}{7+3}$=4.
点评 本题考查了乘法公式、指数幂的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
5.设常数a∈R,集合A={x|x2-(a+1)x+a≥0},B={x|x≥a-1},若A∪B=R,则a的取值范围是( )
| A. | (-∞,2) | B. | (-∞,2] | C. | (2,+∞) | D. | [2,+∞) |
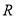 的函数
的函数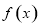 满足下列条件:①对任意的实数
满足下列条件:①对任意的实数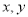 都有:
都有: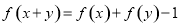 ;②当
;②当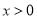 时,
时,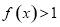 .
.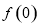 ;
;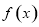 在
在 上为增函数;
上为增函数;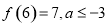 ,关于
,关于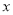 的不等式
的不等式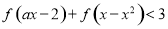 对任意
对任意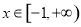 恒成立,求实数
恒成立,求实数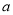 的取值范围.
的取值范围.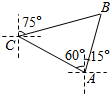 如图所示,一艘海轮从A处出发,测得灯塔在海轮的北偏东15°方向,与海轮相距20海里的B处,海轮按北偏西60°的方向航行了30分钟后到达C处,又测得灯塔在海轮的北偏东75°的方向,则海轮的速度为$\frac{2}{3}$($\sqrt{3}$-1)海里/分钟.
如图所示,一艘海轮从A处出发,测得灯塔在海轮的北偏东15°方向,与海轮相距20海里的B处,海轮按北偏西60°的方向航行了30分钟后到达C处,又测得灯塔在海轮的北偏东75°的方向,则海轮的速度为$\frac{2}{3}$($\sqrt{3}$-1)海里/分钟.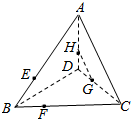 如图,已知点E、F、G、H分别是三棱锥A-BCD棱上的四点,且$\frac{BF}{FC}$=$\frac{BE}{EA}$=$\frac{DH}{HA}$=$\frac{DG}{GC}$=$\frac{1}{2}$.
如图,已知点E、F、G、H分别是三棱锥A-BCD棱上的四点,且$\frac{BF}{FC}$=$\frac{BE}{EA}$=$\frac{DH}{HA}$=$\frac{DG}{GC}$=$\frac{1}{2}$.