题目内容
15.等差数列{an}的首项a1=1,公差d≠0,数列{bn}为等比数列,且b2=a2,b3=a5,b4=a14.(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设数列{cn}对任意n∈N*均有$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{{b}_{2}}$+…+$\frac{{c}_{n}}{{b}_{n}}$=an成立,求c1+c2+…+cn(n≥2)
分析 (I)设等比数列{bn}的公比为q,由于b2=a2,b3=a5,b4=a14.利用等差数列与等比数列的通项公式可得:qb1=1+d,q2b1=1+4d,q3b1=1+13d,联立解得即可.
(II)由于数列{cn}对任意n∈N*均有$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{{b}_{2}}$+…+$\frac{{c}_{n}}{{b}_{n}}$=an成立,可得当n=1时,c1=a1b1.当n≥2时,可得$\frac{{c}_{n}}{{b}_{n}}$=an-an-1=2,可得cn=2×3n-1.再利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(I)设等比数列{bn}的公比为q,
∵b2=a2,b3=a5,b4=a14.
∴qb1=1+d,q2b1=1+4d,q3b1=1+13d,
联立解得b1=1,q=3,d=2.
∴an=1+2(n-1)=2n-1,bn=3n-1.
(II)∵数列{cn}对任意n∈N*均有$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{{b}_{2}}$+…+$\frac{{c}_{n}}{{b}_{n}}$=an成立,
∴当n=1时,c1=a1b1=1.
当n≥2时,$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{{b}_{2}}$+…+$\frac{{c}_{n-1}}{{b}_{n-1}}$=an-1,可得$\frac{{c}_{n}}{{b}_{n}}$=an-an-1=2,
∴cn=2×3n-1.
∴n≥2时,c1+c2+…+cn=1+2(3+32+…+3n-1)=1+2×$\frac{3({3}^{n-1}-1)}{3-1}$=3n-2.
点评 本题考查了“错位相减法”、等比数列与等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

| A. | (-∞,2) | B. | (-∞,2] | C. | (2,+∞) | D. | [2,+∞) |
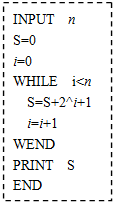
| A. | 36 | B. | 19 | C. | 16 | D. | 10 |
| A. | -1 | B. | 1 | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
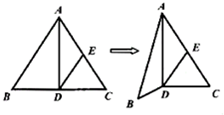 如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )
如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 0 |
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
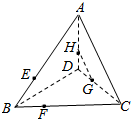 如图,已知点E、F、G、H分别是三棱锥A-BCD棱上的四点,且$\frac{BF}{FC}$=$\frac{BE}{EA}$=$\frac{DH}{HA}$=$\frac{DG}{GC}$=$\frac{1}{2}$.
如图,已知点E、F、G、H分别是三棱锥A-BCD棱上的四点,且$\frac{BF}{FC}$=$\frac{BE}{EA}$=$\frac{DH}{HA}$=$\frac{DG}{GC}$=$\frac{1}{2}$.