题目内容
10.意义运算“*”如下:x*y=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若函数f(x)=(1-2x)*(2x-3)+m的图象与x轴有两个交点,则实数m的取值范围是( )| A. | (-1,+∞) | B. | (-1,1) | C. | [-1,+∞) | D. | [-1,1) |
分析 根据定义求出(1-2x)*(2x-3)的表达式,然后将函数转化为(1-2x)*(2x-3)=-m,利用数形结合即可得到结论.
解答 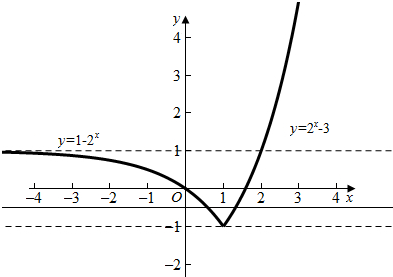 解:由1-2x≥2x-3,即2x≤2,解得x≤1,
解:由1-2x≥2x-3,即2x≤2,解得x≤1,
由1-2x<2x-3,解得x>1,
即(1-2x)*(2x-3)=$\left\{\begin{array}{l}{1-{2}^{x},x≤1}\\{{2}^{x}-3,x>1}\end{array}\right.$,
由f(x)=(1-2x)*(2x-3)+m=0得f(x)=-m,
作出函数y=f(x)与y=-m的图象如图:
要使函数f(x)=(1-2x)*(2x-3)+m的图象与x轴有两个交点,
则满足-m<1或-m>-1,
即-1<m<1,
故选:B.
点评 本题主要考查方程根的个数的应用,利用函数和方程之间的关系,转化为两个函数之间的关系是解决本题的关键.注意要进行数形结合.

练习册系列答案
相关题目
18.海面上有两座灯塔A,B,与观察站C的距离都是m km,灯塔A在观察站C的北偏东40°,灯塔B在观察站C的南偏东20°,则灯塔A,B间的距离是( )
| A. | m km | B. | $\sqrt{2}m\\;km$ km | C. | 2m km | D. | $\sqrt{3}m$ km |
 如图,已知点E、F、G、H分别是三棱锥A-BCD棱上的四点,且$\frac{BF}{FC}$=$\frac{BE}{EA}$=$\frac{DH}{HA}$=$\frac{DG}{GC}$=$\frac{1}{2}$.
如图,已知点E、F、G、H分别是三棱锥A-BCD棱上的四点,且$\frac{BF}{FC}$=$\frac{BE}{EA}$=$\frac{DH}{HA}$=$\frac{DG}{GC}$=$\frac{1}{2}$.