题目内容
11.已知函数f(x)=a+$\frac{1}{{4}^{x}+1}$+$\frac{1}{x}$是奇函数,则函数f(x)的零点个数是2.分析 由函数f(x)=a+$\frac{1}{{4}^{x}+1}$+$\frac{1}{x}$是奇函数可求得a=-$\frac{1}{2}$,从而化为方程2(4x+1)+2x-x(4x+1)=0(x≠0)的解的个数,再由数形结合的思想求解零点个数即可.
解答  解:∵函数f(x)=a+$\frac{1}{{4}^{x}+1}$+$\frac{1}{x}$是奇函数,
解:∵函数f(x)=a+$\frac{1}{{4}^{x}+1}$+$\frac{1}{x}$是奇函数,
∴f(-1)=-f(1),f(-1)=a+$\frac{1}{{4}^{-1}+1}$-1=a-$\frac{1}{5}$,
f(1)=a+$\frac{1}{5}$+1=a+$\frac{6}{5}$,
∴a+$\frac{6}{5}$+a-$\frac{1}{5}$=0,
故a=-$\frac{1}{2}$;
经检验,f(x)=-$\frac{1}{2}$+$\frac{1}{{4}^{x}+1}$+$\frac{1}{x}$是奇函数,
由-$\frac{1}{2}$+$\frac{1}{{4}^{x}+1}$+$\frac{1}{x}$=0得,
2(4x+1)+2x-x(4x+1)=0(x≠0);
∴4x+1=$\frac{2x}{2-x}$;
作函数y=4x+1与函数y=$\frac{2x}{x-2}$的图象如右图,
结合图象可得,
函数f(x)的零点个数是2,
故答案为:2.
点评 本题考查了函数奇偶性的判断与应用及方程的根与函数的零点的关系应用,同时考查了数形结合的思想应用,属于中档题.

练习册系列答案
相关题目
1.点M(6,-2$\sqrt{3}$)的极坐标为( )
| A. | (4$\sqrt{3}$,$\frac{π}{6}$) | B. | (4$\sqrt{3}$,$\frac{π}{3}$) | C. | (4$\sqrt{3}$,$\frac{11π}{6}$) | D. | (4$\sqrt{3}$,-$\frac{π}{6}$) |
2.P点的直角坐标(-1,$\sqrt{3}$)化成极坐标为( )
| A. | (2,$\frac{2}{3}$π) | B. | ($\sqrt{2}$,$\frac{2}{3}$π) | C. | ($\sqrt{2}$,$\frac{4}{3}$π) | D. | (2,$\frac{4}{3}$π) |
19.已知,P(A)=0.3,P(B|A)=0.4,P(A|B)=0.2,则P(A+B)=( )
(其中P(A+B)=P(A)+P(B)-P(AB))
(其中P(A+B)=P(A)+P(B)-P(AB))
| A. | 0.90 | B. | 0.78 | C. | 0.60 | D. | 0.40 |
20.将两枚质地均匀的骰子各掷一次,设事件A={两个点数互不相同},B={出现一个5点},则P(B|A)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
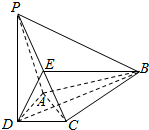 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.