题目内容
【题目】已知函数y=f(x)定义在实数集R上的奇函数,当x≥0时,函数y=f(x)的图象如图所示(抛物线的一部分). 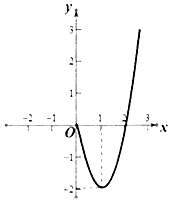
(1)在原图上画出x<0时函数y=f(x)的示意图;
(2)求函数y=f(x)的解析式(不要求写出解题过程);
(3)写出函数y=|f(x)|的单调递增区间(不要求写出解题过程).
【答案】
(1)解: 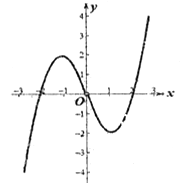
(2)解:x≥0时,函数y=f(x)的图象如图,
可知函数的对称轴为:x=1,f(2)=0,f(0)=0,f(1)=﹣2,
可得x≥0时,f(x)=2(x﹣1)2﹣2=2x2﹣4x.
函数是奇函数,x<0时,f(x)=﹣f(﹣x)=﹣2x2﹣4x.
∴ ![]()
(3)解:y=|f(x)|的单调递增区间为:(﹣2,﹣1),(0,1),(2,+∞)
【解析】(1)利用函数的奇偶性补齐函数的图象即可.(2)利用函数的奇偶性求解函数的解析式即可.(3)结合函数的图象直接写出函数的单调增区间即可.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目