题目内容
【题目】(不等式选讲)
已知函数![]() .
.
(1)若![]() ,解不等式
,解不等式![]() ;
;
(2)若不等式![]() 在R上恒成立,求实数
在R上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)[2,+∞).(2){a|a≥2或a≤-4}.
【解析】试题分析:(1)分x<-1,-1≤x≤3,x>3三种情况去掉绝对值讨论即可.
(2)由绝对值三角不等式的性质可得|x+a|+|x-1|≥|a+1|,只需|a+1|≥3,求解即可.
试题解析:(1)依题意,|x+1|+|x-3|≤2x.
当x<-1时,原不等式化为-1-x+3-x≤2x,解得x≥![]() ,故无解;
,故无解;
当-1≤x≤3时,原不等式化为x+1+3-x≤2x,解得x≥2,故2≤x≤3;
当x>3时,原不等式化为x+1+x-3≤2x,即-2≤0恒成立.
综上所述,不等式f(x)+|x-3|≤2x的解集为[2,+∞).
(2)f(x)+|x-1|≥3|x+a|+|x-1|≥3恒成立,
由|x+a|+|x-1|≥|a+1|可知,只需|a+1|≥3即可,
故a≥2或a≤-4,即实数a的取值范围为{a|a≥2或a≤-4}.

【题目】设连续掷两次骰子得到的点数分别为m、n,令平面向量 ![]() ,
, ![]() .
.
(1)求使得事件“ ![]() ”发生的概率;
”发生的概率;
(2)求使得事件“ ![]() ”发生的概率;
”发生的概率;
(3)使得事件“直线 ![]() 与圆(x﹣3)2+y2=1相交”发生的概率.
与圆(x﹣3)2+y2=1相交”发生的概率.
【题目】如表中给出了2011年~2015年某市快递业务总量的统计数据(单位:百万件)
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
快递业务总量 | 34 | 55 | 71 | 85 | 105 |
(1)在图中画出所给数据的折线图; 
(2)建立一个该市快递量y关于年份代码x的线性回归模型;
(3)利用(2)所得的模型,预测该市2016年的快递业务总量.
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:
斜率: 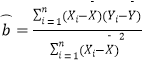 ,纵截距:
,纵截距: ![]() .
.