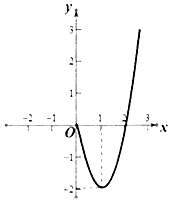
��Ŀ����
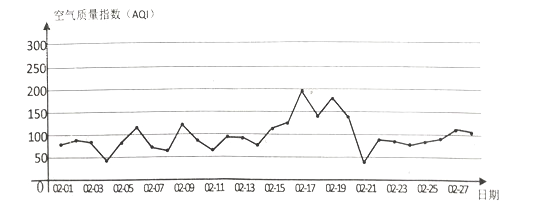
����Ŀ����ͼΪij��2017��2��28����տ�������ָ������ͼ.
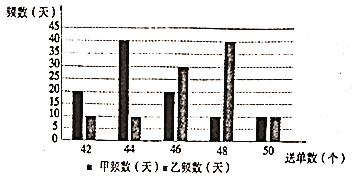
���й�����������������ƽ̨�ṩ�Ŀ�������ָ�������£�

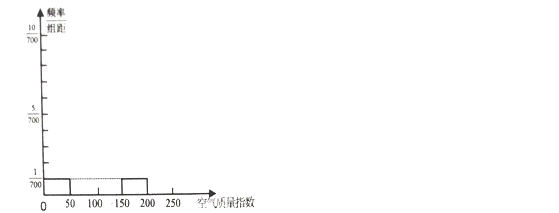
��1�����������������ͼ��ȫ�·���Ƶ�ʷֲ�ֱ��ͼ������Ǧ��Ϳ�ھ����������������2�·ݿ�������ָ��������ݵ�ƽ����������С�����һλ����
��2���о���Ա���֣���������ָ��������![]() ��ȼ���ŷŵ�
��ȼ���ŷŵ�![]() ������Ŀ����������ع�ϵ����
������Ŀ����������ع�ϵ����![]() Ϊ��λ���±�����
Ϊ��λ���±�����![]() ��
��![]() ��������ݣ�
��������ݣ�

��![]() ����
����![]() �Ļع鷽�̣������Ƶ�
�Ļع鷽�̣������Ƶ�![]() �ŷ�����
�ŷ�����![]() ʱ��
ʱ�� ![]() ��ֵ.
��ֵ.
������С���˷���ع鷽�̵�ϵ����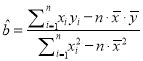 ��
�� ![]() ��
��
���𰸡���1��92.9;(2) ![]() ��
�� ![]() .
.
�������������������1����������ͼ���Ƶ�����Ӷ��������Ƶ�ʣ��������ɵ������꣬�����ɲ�ȫֱ��ͼ��(2)�ɹ�ʽ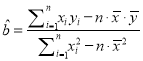 �����ɵ�
�����ɵ�![]() ��ֵ�������������ĵ��������
��ֵ�������������ĵ��������![]() ���ɵ�
���ɵ�![]() ��ֵ�������ûع鷽�̣���
��ֵ�������ûع鷽�̣���![]() ����ع鷽�̼��ɵý��.
����ع鷽�̼��ɵý��.
�����������1�� ������ͼ��֪����������ָ��Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��Ƶ���ֱ�Ϊ2��16��8��2��������Ӧ��Ƶ�ʷֱ�Ϊ
��Ƶ���ֱ�Ϊ2��16��8��2��������Ӧ��Ƶ�ʷֱ�Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��С���εĸ߷ֱ�Ϊ
��С���εĸ߷ֱ�Ϊ![]() .
.
������ͼ���£�
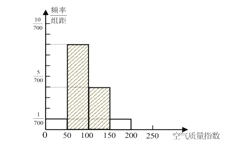
����2�·ݿ�������ָ��������ݵ�ƽ��������Ϊ
![]() .
.
��2���ɱ������ݿ�֪��
![]() ��
�� ![]() ��
�� ![]()
![]() ��
��
��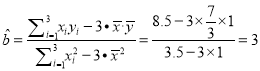 ��
��
![]()
![]() ��
��
��![]() ����
����![]() �Ļع鷽��Ϊ
�Ļع鷽��Ϊ![]() ��
��
��![]() ʱ�����
ʱ�����![]() ��
��
![]() ��CO�ŷ�����
��CO�ŷ�����![]() ʱ��PM2.5��ֵ����Ϊ
ʱ��PM2.5��ֵ����Ϊ![]() .
.

 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�����Ŀ��PM2.5��ָ������ֱ��С�ڻ����2.5�Ŀ����Ҳ�ƿ���ο������Ϊ��̽����������PM2.5��Ũ���Ƿ���أ��ֲɼ���ij������һ������ijһʱ��γ�������PM2.5�����������
ʱ�� | ��һ | �ܶ� | ���� | ���� | ���� |
������x�������� | 50 | 51 | 54 | 57 | 58 |
PM2.5��Ũ��y����/�����ף� | 69 | 70 | 74 | 78 | 79 |
��1�������ϱ����ݣ�������ͼ����ϵ�л���ɢ��ͼ�� 
��2�������ϱ����ݣ�����С���˷����y����x�����Իع鷽�� ![]() ��������2λС����
��������2λС����
��3��������ͬһʱ��γ�������25�������Ը��ݣ�2����������Իع鷽��Ԥ�⣬��ʱPM2.5��Ũ��Ϊ���٣�������������
�ο���ʽ�� ![]() =
= 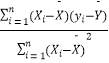 ��
�� ![]() =
= ![]() ��
�� ![]()
![]() ��
��
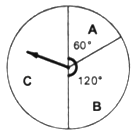
����Ŀ���ҹ����̻���Ŀ���࣬��ɫƷ�ַ��ӣ����С��ջ����̻�����׳�۵��̻�֮һ������ʱһ�������������ﵽ��ߵ�ʱ���ѣ�ͨ���о������ָ����̻�����ʱ�����ĸ߶�h����λ���ף���ʱ��t����λ���룩���ں�����ϵ�����õ�����������±���
ʱ��t |
| 2 | 4 |
�߶�h | 10 | 25 | 17 |
�� I�������ϱ����ݣ������к����У�ѡȡһ���������������̻�����ʱ�����ĸ߶�h��ʱ��t�ı仯��ϵ��y1=kt+b��y2=at2+bt+c��y3=abt �� ȷ���˺�������ʽ������˵�����ɣ�
�� II��������ѡȡ�ĺ������ж��̻����ѵ����ʱ�̣��������ʱ�̻������ĸ߶ȣ�