题目内容
【题目】设椭圆
的左顶点为
，且椭圆
与直线
相切，
（1）求椭圆
的标准方程；
（2）过点
的动直线与椭圆
交于
两点，设
为坐标原点，是否存在常数
，使得
？请说明理由.
【答案】（1）
（2）-7
【解析】试题分析：
(1)利用题意求得
，则椭圆的标准方程为
(2)当直线斜率存在时，联立直线与椭圆方程进行讨论，注意讨论直线不存在的情况，综上可得当
时， 
试题解析：
（1）根据题意可知
，所以
，
由椭圆
与直线
相切，联立得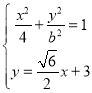
，
消去
可得： 
，
即
，
解得： 
（舍）或
所以椭圆的标准方程为
（2）当过点
的直线
的斜率存在时，设直线
的方程为
，设
两点的坐标分别为
，
联立得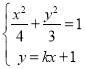
，化简
，
所以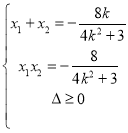
，
所以
，
所以当
时， 
当过点
的直线
的斜率不存在时，直线即与
轴重合，此时
，所以
,
所以当
时， 
,
综上所述，当
时， 
名师伴你成长课时同步学练测系列答案【题目】“特罗卡”是靶向治疗肺癌的一种药物，为了研究其疗效，医疗专家借助一些肺癌患者，进行人体试验，得到如右丢失一些数据的2×2列联表：
疫苗效果试验列
感染 | 未感染 | 总计 | |
没服用 | 20 | 30 | 50 |
服用 | X | y | 50 |
总计 | M | N | 100 |
设从没服用该药物的肺癌患者中任选两人，未感染人数为ξ；从服用该药物的肺癌患者中任选两人，未感染人数为η，研究人员曾计算过得出：P（ξ=0）= 
P（η=0）．
（1）求出列联表中数据x，y，M，N的值．
（2）能否有97.5%的把握认为该药物对治疗肺癌有疗效吗？
P（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
注：K2= 
．
【题目】如表中给出了2011年～2015年某市快递业务总量的统计数据（单位：百万件）
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
快递业务总量 | 34 | 55 | 71 | 85 | 105 |
（1）在图中画出所给数据的折线图； 
（2）建立一个该市快递量y关于年份代码x的线性回归模型；
（3）利用（2）所得的模型，预测该市2016年的快递业务总量．
附：回归直线方程的斜率和截距的最小二乘估计公式分别为：
斜率：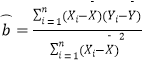 
，纵截距： 
．
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物（也称可入肺颗粒物）．为了探究车流量与PM2.5的浓度是否相关，现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表：
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量x（万辆） | 50 | 51 | 54 | 57 | 58 |
PM2.5的浓度y（微克/立方米） | 69 | 70 | 74 | 78 | 79 |
（1）根据上表数据，请在如图坐标系中画出散点图； 
（2）根据上表数据，用最小二乘法求出y关于x的线性回归方程 
；（保留2位小数）
（3）若周六同一时间段车流量是25万辆，试根据（2）求出的线性回归方程预测，此时PM2.5的浓度为多少（保留整数）？
参考公式： 
= 
， 
= 
﹣ 
．
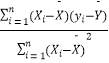