题目内容
【题目】已知△ABC的内角A，B，C的对边分别为a，b，c，且2csinBcosA﹣bsinC=0．
（1）求角A；
（2）若△ABC的面积为 
，b+c=5，求a．
【答案】
（1）解：在△ABC中，由2csinBcosA﹣bsinC=0及正弦定理得：2sinCsinBcosA﹣sinBsinC=0，
∵0＜B＜π，0＜C＜π，sinBsinC≠0，
∴2cosA=1，即 
．
又0＜A＜π， 
．
（2）解： 
，又∵ ，∴ 
，∴bc=4，
由余弦定理得a2=b2+c2﹣2bccosA=（b+c）2﹣3bc=25﹣12=13，
∴ 
．
【解析】（1）由2csinBcosA﹣bsinC=0及正弦定理求得2cosA=1，即 ，从而求得A的值．（2）由 ，求得bc=4，再由余弦定理求得a2的值，可得a的值．
练习册系列答案
相关题目
【题目】如表中给出了2011年～2015年某市快递业务总量的统计数据（单位：百万件）
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
快递业务总量 | 34 | 55 | 71 | 85 | 105 |
（1）在图中画出所给数据的折线图； 
（2）建立一个该市快递量y关于年份代码x的线性回归模型；
（3）利用（2）所得的模型，预测该市2016年的快递业务总量．
附：回归直线方程的斜率和截距的最小二乘估计公式分别为：
斜率：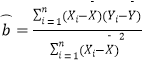 
，纵截距： 
．
