题目内容
“若存在一条与函数y=f(x)的图象有两个不同交点P(x1,y1),Q(x2,y2)的直线,使y=f(x)在x=
处的切线与此直线平行”,则称这样的函数y=f(x)为“hold函数”;下列函数:
①y=
;②y=x2(x>0);③y=
;④y=lnx;
其中为“hold函数”的是( )
| x1+x2 |
| 2 |
①y=
| 1 |
| x |
| 1-x2 |
其中为“hold函数”的是( )
| A、①②④ | B、②③ |
| C、③④ | D、①③④ |
考点:利用导数研究曲线上某点切线方程,函数的概念及其构成要素
专题:导数的综合应用
分析:(1)设一条直线l与函数f(x)=
的图象有两个不同交点P(x1,y1),Q(x2,y2)(x1≠x2)的直线,可得kl=
=-
.由于f′(x)=-
,可得y=f(x)在x=
处的切线的斜率k=f′(
)=-
,可得-
≠-
,因此函数f(x)=
不是“hold函数”;
(2)设一条直线l与函数f(x)=x2(x>0)的图象有两个不同交点P(x1,y1),Q(x2,y2)的直线,可得kl=
=x2+x1.由于f′(x)=2x,可得y=f(x)在x=
处的切线的斜率k=f′(
)=x1+x2,即可判断出.
同理可判定:(3)为“hold函数”;(4)不为“hold函数”.
| 1 |
| x |
| y2-y1 |
| x2-x1 |
| 1 |
| x1x2 |
| 1 |
| x2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 4 |
| (x1+x2)2 |
| 1 |
| x1x2 |
| 4 |
| (x1+x2)2 |
| 1 |
| x |
(2)设一条直线l与函数f(x)=x2(x>0)的图象有两个不同交点P(x1,y1),Q(x2,y2)的直线,可得kl=
| y2-y1 |
| x2-x1 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
同理可判定:(3)为“hold函数”;(4)不为“hold函数”.
解答:
解:(1)设一条直线l与函数f(x)=
的图象有两个不同交点P(x1,y1),Q(x2,y2)(x1≠x2)的直线,则kl=
=
=-
,
∵f′(x)=-
,∴y=f(x)在x=
处的切线的斜率k=f′(
)=-
,假设-
=-
,可得x1=x2,与已知x1≠x2矛盾,因此函数f(x)=
不是
“hold函数”;
(2)设一条直线l与函数f(x)=x2(x>0)的图象有两个不同交点P(x1,y1),Q(x2,y2)的直线,则kl=
=
=x2+x1,
∵f′(x)=2x,∴y=f(x)在x=
处的切线的斜率k=f′(
)=2×
=x1+x2,
∴存在一条直线l与函数y=f(x)的图象有两个不同交点P(x1,y1),Q(x2,y2)的直线,使y=f(x)在x=
处的切线与此直线平行,
因此函数f(x)=x2为“hold函数”;
同理可判定:(3)为“hold函数”;(4)不为“hold函数”.
故选:B.
| 1 |
| x |
| y2-y1 |
| x2-x1 |
| ||||
| x2-x1 |
| 1 |
| x1x2 |
∵f′(x)=-
| 1 |
| x2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 4 |
| (x1+x2)2 |
| 1 |
| x1x2 |
| 4 |
| (x1+x2)2 |
| 1 |
| x |
“hold函数”;
(2)设一条直线l与函数f(x)=x2(x>0)的图象有两个不同交点P(x1,y1),Q(x2,y2)的直线,则kl=
| y2-y1 |
| x2-x1 |
| ||||
| x2-x1 |
∵f′(x)=2x,∴y=f(x)在x=
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
∴存在一条直线l与函数y=f(x)的图象有两个不同交点P(x1,y1),Q(x2,y2)的直线,使y=f(x)在x=
| x1+x2 |
| 2 |
因此函数f(x)=x2为“hold函数”;
同理可判定:(3)为“hold函数”;(4)不为“hold函数”.
故选:B.
点评:本题考查了新定义“hold函数”、直线的斜率计算公式、利用导数研究函数切线的斜率,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
| 1+2sin500°cos500° |
| A、sin40°-cos40° |
| B、cos40°-sin40° |
| C、sin40°+cos40° |
| D、sin40°•cos40° |
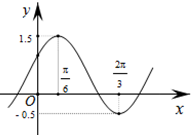 已知函数y=Asin(ωx+φ)+b的一部分图象如图所示,若A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ)+b的一部分图象如图所示,若A>0,ω>0,|φ|< 如图,E,F是边长为3的正方形ABCD的边AD上两个点,且AE=DF.连接CF交BD于G,连接BE交AG于点H,若|CH|2:|CE|2=9:10,则AE的长为
如图,E,F是边长为3的正方形ABCD的边AD上两个点,且AE=DF.连接CF交BD于G,连接BE交AG于点H,若|CH|2:|CE|2=9:10,则AE的长为