题目内容
函数f(x)=
,则函数y=f(x)-
的零点是 .
|
| 1 |
| 4 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:令f(x)-
=0,分类讨论解方程即可求得结果.
| 1 |
| 4 |
解答:
解:当x≥1时,2x-2-
=0解得x=
;
当x<1时,x2-2x-
=0解得x=
故答案为:
或
| 1 |
| 4 |
| 9 |
| 8 |
当x<1时,x2-2x-
| 1 |
| 4 |
1-
| ||
| 2 |
故答案为:
| 9 |
| 8 |
1-
| ||
| 2 |
点评:此题是基础题.考查函数的零点与方程根之间的关系.体现了转化和分类讨论的思想,以及考查了学生的计算能力.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
| 1+2sin500°cos500° |
| A、sin40°-cos40° |
| B、cos40°-sin40° |
| C、sin40°+cos40° |
| D、sin40°•cos40° |
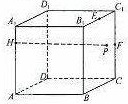 如图,已知正方体ABCD-A1B1C1D1的棱长为4,点H在棱AA1上,且HA1=1,点E、F分别为B1C1、CC1的中点,P为侧面BCC1B1上一动点,且PE⊥PF,则当点P运动时,求HP2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为4,点H在棱AA1上,且HA1=1,点E、F分别为B1C1、CC1的中点,P为侧面BCC1B1上一动点,且PE⊥PF,则当点P运动时,求HP2的最小值是( )| A、9 | ||
B、27--6
| ||
C、51-14
| ||
D、14-3
|