题目内容
【题目】已知有穷数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .若数列
.若数列![]() 中各项都是集合
中各项都是集合![]() 的元素,则称该数列为
的元素,则称该数列为![]() 数列.对于
数列.对于![]() 数列
数列![]() ,定义如下操作过程
,定义如下操作过程![]() :从
:从![]() 中任取两项
中任取两项![]() ,
,![]() ,将
,将![]() 的值添在
的值添在![]() 的最后,然后删除
的最后,然后删除![]() ,
,![]() ,这样得到一个
,这样得到一个![]() 项的新数列
项的新数列![]() (约定:一个数也视作数列).若
(约定:一个数也视作数列).若![]() 还是
还是![]() 数列,可继续实施操作过程
数列,可继续实施操作过程![]() ,得到的新数列记作
,得到的新数列记作![]() ,
,![]() ,如此经过
,如此经过![]() 次操作后得到的新数列记作
次操作后得到的新数列记作![]() .
.
(1)设![]() ,
,![]() ,
,![]() 请写出
请写出![]() 的所有可能的结果;
的所有可能的结果;
(2)求证:对于一个![]() 项的
项的![]() 数列
数列![]() 操作
操作![]() 总可以进行
总可以进行![]() 次;
次;
(3)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 求
求![]() 的可能结果,并说明理由.
的可能结果,并说明理由.
【答案】(1)![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() .;(2)证明见解析;(3)
.;(2)证明见解析;(3)![]()
【解析】
(1)直接按定义来操作,每次取两个数代入计算即可求出![]() 的所有可能的结果;
的所有可能的结果;
(2)先通过作差得到每次操作后新数列仍是![]() 数列;再根据每次操作中都是增加一项,删除两项即可得到结论;
数列;再根据每次操作中都是增加一项,删除两项即可得到结论;
(3)先定义运算:![]() ,并证明这种运算满足交换律和结合律;再结合(2)可知
,并证明这种运算满足交换律和结合律;再结合(2)可知![]() 中仅有一项,再按定义先求出
中仅有一项,再按定义先求出![]() ,综合即可得到
,综合即可得到![]() 的可能结果.
的可能结果.
(1)直接按定义来操作,当取0,![]() 时代入计算可得:
时代入计算可得:![]() ,
,![]() ;
;
当取0,![]() 时可得
时可得![]() ,
,![]() ;
;
当取![]() ,
,![]() 时,可得
时,可得![]() ,
,![]() .
.
故有如下的三种可能结果:![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() .
.
(2)因为对![]() ,
,![]() ,有
,有
![]() 且
且![]()
所以![]() ,即每次操作后新数列仍是
,即每次操作后新数列仍是![]() 数列.
数列.
又由于每次操作中都是增加一项,删除两项,
所以对![]() 数列
数列![]() 每操作一次,项数就减少一项,
每操作一次,项数就减少一项,
所以对![]() 项的
项的![]() 数列
数列![]() 可进行
可进行![]() 次操作(最后只剩下一项).
次操作(最后只剩下一项).
(3)由(2)可知![]() 中仅有一项.
中仅有一项.
对于满足![]() ,
,![]() 的实数
的实数![]() ,
,![]() 定义运算:
定义运算:![]() ,
,
下面证明这种运算满足交换律和结合律.
因为![]() ,且
,且![]() ,所以
,所以![]() ,即该运算满足交换律;
,即该运算满足交换律;
因为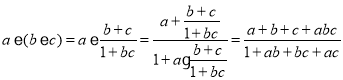
且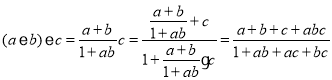
所以![]() ,即该运算满足结合律.
,即该运算满足结合律.
所以![]() 中的项与实施的具体操作过程无关,
中的项与实施的具体操作过程无关,
选择如下操作过程求![]()
由(1)可知![]() ;
;
易知![]() ,
,![]() ,
,![]() ,
,![]() ;
;
所以![]() ,0,0,0,0;
,0,0,0,0;
易知![]() 经过4次操作后剩下一项为
经过4次操作后剩下一项为![]() .
.
综上可知:![]() .
.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目