Question

【题目】已知数列的前项和为，当时，满足.

（1）求证：；

（2）求证：数列为等差数列；

（3）若，公差，问是否存在，，使得？如果存在，求出所有满足条件的，，如果不在，请说明理由.

Answer 1

【答案】（1）证明见解析（2）证明见解析（3）存在，或.

【解析】

（1）已知条件是时，，令可证结论；

（2）已知条件变形

，用累加的方法得，从而，把此式再写一次：

当时，，两式相减得：时，，同时也适合此式，从而证明是等差数列；

（3）由求得，让从2开始一一检验，看是否有，当然时，有，.

（1）证明：∵时，，

令得，，

∴.

（2）由

，

∴，

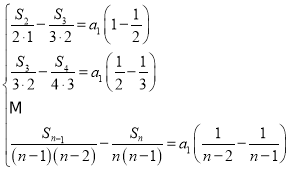各式相加得，，

当时，，

由时，，

而，，也满足上式，∴为等差数列.

（3）∵，公差为，

∴，，，

当时，，当时，，

当时，（舍），时，（舍），

当时，（舍），时，（舍），

当时，（舍），

当时，，

∴，（舍），

综上或.