题目内容
【题目】已知数列![]() 的前
的前![]() 项积为
项积为![]() ,满足
,满足![]() . 数列
. 数列![]() 的首项为
的首项为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)记集合![]() ,若集合
,若集合![]() 的元素个数为
的元素个数为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在正整数![]() 使得
使得![]() 成立?如果存在,请写出
成立?如果存在,请写出![]() 满足的条件,如果不存在,请说明理由.
满足的条件,如果不存在,请说明理由.
【答案】(1)![]() ,bn=2n;(2)
,bn=2n;(2)![]() ;(3)答案不唯一,见解析
;(3)答案不唯一,见解析
【解析】
(1)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,即可的
,即可的![]() 的通项公式,由
的通项公式,由![]() 可得
可得![]() ,即数列
,即数列![]() 是常数数列,即可求出
是常数数列,即可求出![]() 的通项公式;
的通项公式;
(2)参变分离,构造函数列![]() ,判断其增减性,即可求出
,判断其增减性,即可求出![]() 的取值范围;
的取值范围;
(3)假设存在,根据数列![]() 为等比数列,利用公式求出其前
为等比数列,利用公式求出其前![]() 项和,对
项和,对![]() 分类讨论.
分类讨论.
(1)因为![]() ,所以当
,所以当![]() 时,
时,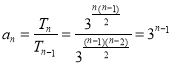
而当![]() 时,
时,![]() 适合上式,所以
适合上式,所以![]() ,因为
,因为![]() ,即
,即![]()
所以数列![]() 是常数数列,所以
是常数数列,所以![]() ,所以
,所以![]() .
.
(2)由(1)知,不等式![]() 即为
即为![]()
设![]()
因为![]()
![]()
而![]()
要使![]() 只有2解,则有
只有2解,则有![]()
(3)假设存在正整数![]() ,因为
,因为![]()
所以有![]() 若
若![]() ,则
,则![]() 不成立,
不成立,
所以![]() ,
,![]() ,若
,若![]() 为奇数,当
为奇数,当![]() 时,
时,![]() ,不成立,.
,不成立,.
当![]() 时,设
时,设![]() ,
,![]() , 则
, 则![]() .
.
若q为偶数,设![]() ,
,![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() .
.
综上所述,当![]() 为大于1的奇数时,
为大于1的奇数时,![]() ,
,![]() ;
;
当q为偶数时,不存在.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】某区在2019年教师招聘考试中,参加![]() 、
、![]() 、
、![]() 、
、![]() 四个岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
四个岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
岗位 | 男性应聘人数 | 男性录用人数 | 男性录用比例 | 女性应聘人数 | 女性录用人数 | 女性录用比例 |
| 269 | 167 | 62% | 40 | 24 | 60% |
| 217 | 69 | 32% | 386 | 121 | 31% |
| 44 | 26 | 59% | 38 | 22 | 58% |
| 3 | 2 | 67% | 3 | 2 | 67% |
总计 | 533 | 264 | 50% | 467 | 169 | 36% |
(1)从表中所有应聘人员中随机抽取1人,试估计此人被录用的概率;
(2)将应聘![]() 岗位的男性教师记为
岗位的男性教师记为![]() ,女性教师记为
,女性教师记为![]() ,现从应聘
,现从应聘![]() 岗位的6人中随机抽取2人.
岗位的6人中随机抽取2人.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2人性别不同”,求事件
为事件“抽取的2人性别不同”,求事件![]() 发生的概率.
发生的概率.