题目内容
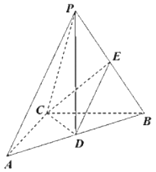
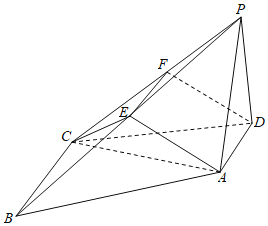
【题目】如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD//BC,BC=2AD,AD⊥CD,PD⊥平面ABCD,E为PB的中点.
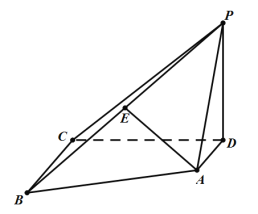
(1)求证:AE//平面PDC;
(2)若BC=CD=PD,求直线AC与平面PBC所成角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() ,推导出四边形
,推导出四边形![]() 是平行四边形,从而
是平行四边形,从而![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
(2)推导出![]() ,由
,由![]() ,得
,得![]() ,再推导出
,再推导出![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,进而
,进而![]() 平面
平面![]() ,连结
,连结![]() ,
,![]() ,则
,则![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成角,由此能求出直线
所成角,由此能求出直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
解:(1)证明:取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() ,
,
![]() 是
是![]() 的中点,
的中点,![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
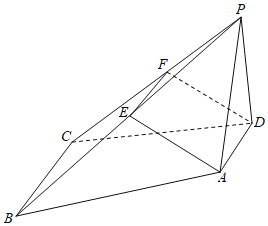
(2)解:![]() ,
,![]() 是等腰三角形,
是等腰三角形,
![]() ,又
,又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
连结![]() ,
,![]() ,则
,则![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成角,
所成角,
设![]() ,
,
在![]() 中,解得
中,解得![]() ,
,![]() ,
,![]() ,
,
在![]() 中,解得
中,解得![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]() 直线
直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】某市一所医院在某时间段为发烧超过38![]() 的病人特设发热门诊,该门诊记录了连续5天昼夜温差
的病人特设发热门诊,该门诊记录了连续5天昼夜温差![]() (
(![]() )与就诊人数
)与就诊人数![]() 的资料:
的资料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
昼夜温差 | 8 | 10 | 13 | 12 | 7 |
就诊人数 | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相关系数
的相关系数![]() ,并说明昼夜温差(
,并说明昼夜温差(![]() )与就诊人数
)与就诊人数![]() 具有很强的线性相关关系.
具有很强的线性相关关系.
(2)求就诊人数![]() (人)关于出昼夜温差
(人)关于出昼夜温差![]() (
(![]() )的线性回归方程,预测昼夜温差为9
)的线性回归方程,预测昼夜温差为9![]() 时的就诊人数.
时的就诊人数.
附:样本![]()
![]() 的相关系数为
的相关系数为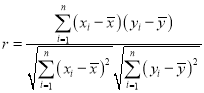 ,当
,当![]() 时认为两个变量有很强的线性相关关系.
时认为两个变量有很强的线性相关关系.
回归直线方程为![]() ,其中
,其中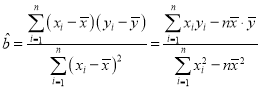 ,
,![]() .
.
参考数据:![]() ,
,![]()
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某市一所医院在某时间段为发烧超过38![]() 的病人特设发热门诊,该门诊记录了连续5天昼夜温差
的病人特设发热门诊,该门诊记录了连续5天昼夜温差![]() (
(![]() )与就诊人数
)与就诊人数![]() 的资料:
的资料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
昼夜温差 | 8 | 10 | 13 | 12 | 7 |
就诊人数 | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相关系数
的相关系数![]() ,并说明昼夜温差(
,并说明昼夜温差(![]() )与就诊人数
)与就诊人数![]() 具有很强的线性相关关系.
具有很强的线性相关关系.
(2)求就诊人数![]() (人)关于出昼夜温差
(人)关于出昼夜温差![]() (
(![]() )的线性回归方程,预测昼夜温差为9
)的线性回归方程,预测昼夜温差为9![]() 时的就诊人数.
时的就诊人数.
附:样本![]()
![]() 的相关系数为
的相关系数为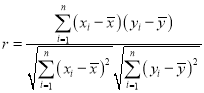 ,当
,当![]() 时认为两个变量有很强的线性相关关系.
时认为两个变量有很强的线性相关关系.
回归直线方程为![]() ,其中
,其中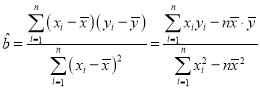 ,
,![]() .
.
参考数据:![]() ,
,![]()