题目内容
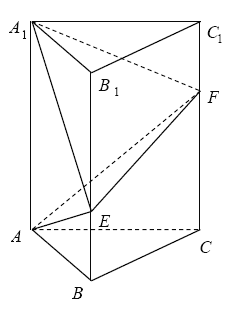
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,点E,F分别在
,点E,F分别在![]() ,
,![]() ,且
,且![]() ,
,![]() .设
.设![]() .
.
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)当平面![]() 平面
平面![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)60°(2)![]()
【解析】
(1)推导出![]() 平面ABC,
平面ABC,![]() AC,建立分别以AB,AC,
AC,建立分别以AB,AC,![]() 为
为![]() 轴的空间直角坐标系,利用法向量能求出异面直线AE与
轴的空间直角坐标系,利用法向量能求出异面直线AE与![]() 所成角.
所成角.
(2)推导出平面![]() 的法向量和平面
的法向量和平面![]() 的一个法向量,由平面
的一个法向量,由平面![]() 平面
平面![]() ,能求出
,能求出![]() 的值.
的值.
解:因为直三棱柱![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
又因为![]() ,
,
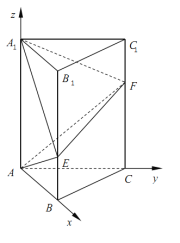
所以建立分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴的空间直角坐标系
轴的空间直角坐标系![]() .
.
(1)设![]() ,则
,则![]() ,
,![]() ,
,
各点的坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.
因为![]() ,
,![]() ,
,
所以 .
.
所以向量![]() 和
和![]() 所成的角为120°,
所成的角为120°,
所以异面直线![]() 与
与![]() 所成角为60°;
所成角为60°;
(2)因为![]() ,
,![]() ,
,
![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,且
,且![]() .
.
即![]() ,且
,且![]() .
.
令![]() ,则
,则![]() ,
,![]() .
.
所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
同理,![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
因为平面![]() 平面
平面![]() ,
,
所以![]() ,
,
![]() ,
,
解得![]() .
.
所以当平面![]() 平面
平面![]() 时,
时,![]() .
.

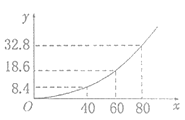
【题目】2014年12月19日,2014年中国数学奥林匹克竞赛(第30届全国中学生数学冬令营)在重庆市巴蜀中学举行.参加本届中国数学奥林匹克竞赛共有来自各省、市(自治区、直辖市)、香港地区、澳门地区,以及俄罗斯、新加坡等国的30余支代表队,共317名选手.竞赛为期2天,每天3道题,限时4个半小时完成.部分优胜者将参加为国际数学奥林匹克竞赛而组建的中国国家集训队.中国数学奥林匹克竞赛(全国中学生数学冬令营)是在全国高中数学联赛基础上进行的一次较高层次的数学竞赛,该项活动也是中国中学生级别最高、规模最大、最有影响的全国性数学竞赛.2020年第29届全国中学生生物学竞赛也将在重庆巴蜀中学举行.巴蜀中学校本选修课“数学建模”兴趣小组调查了2019年参加全国生物竞赛的200名学生(其中男生、女生各100人)的成绩,得到这200名学生成绩的中位数为78.这200名学生成绩均在50与110之间,且成绩在![]() 内的人数为30,这200名学生成绩的高于平均数的男生有62名,女生有38名.并根据调查结果画出如图所示的频率分布直方图.
内的人数为30,这200名学生成绩的高于平均数的男生有62名,女生有38名.并根据调查结果画出如图所示的频率分布直方图.
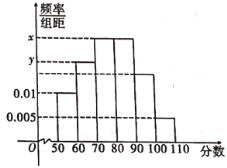
(1)求![]() ,
,![]() 的值;
的值;
(2)填写下表,能否有![]() 的把握认为学生成绩是否高于平均数与性别有关系?
的把握认为学生成绩是否高于平均数与性别有关系?
男生 | 女生 | 总计 | |
成绩不高于平均数 | |||
成绩高于平均数 | |||
总计 |
参考公式及数据: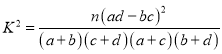 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |