题目内容
6.已知tan(π-α)=-2,则$\frac{1}{{cos2α+{{cos}^2}α}}$=( )| A. | -3 | B. | $\frac{2}{5}$ | C. | 3 | D. | $-\frac{5}{2}$ |
分析 由条件利用诱导公式求得tanα的值,再利用同角三角函数的基本关系求得所给式子的值.
解答 解:∵tan(π-α)=-tanα=-2,∴tanα=2,
∴$\frac{1}{{cos2α+{{cos}^2}α}}$=$\frac{{sin}^{2}α{+cos}^{2}α}{{2cos}^{2}α{-sin}^{2}α}$=$\frac{{tan}^{2}α+1}{2{-tan}^{2}α}$=$\frac{4+1}{2-4}$=-$\frac{5}{2}$,
故选:D.
点评 本题主要考查同角三角函数的基本关系的应用,诱导公式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-3,2),且向量k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$平行,则实数k的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
18.“m=3”是“函数f(x)=xm为实数集R上的奇函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
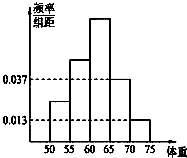 为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.