题目内容
11.已知f(x)的定义域为[-π,π],且f(x)为偶函数,且当x∈[0,π]时,f(x)=2sin(x+$\frac{π}{3}$).(1)求f(x)的解析式及f(x)的单调增区间;
(2)若[f(x)]2-$\sqrt{3}$f(x)=0,求x的所有可能取值.
分析 (1)根据偶函数满足f(-x)=f(x),求出当x∈[-π,0]时的解析式,即可得到f(x)的解析式,画出函数图象,易得f(x)的单调增区间;
(2)若[f(x)]2-$\sqrt{3}$f(x)=0,则f(x)=0或f(x)=$\sqrt{3}$,进而可得x的取值
解答 解:(1)当x∈[-π,0]时,-x∈[0,π],
f(-x)=2sin(-x+$\frac{π}{3}$)
由于f(x)为偶函数,则f(-x)=f(x),
故f(x)=2sin(-x+$\frac{π}{3}$)x∈[-π,0]
即f(x)=$\left\{\begin{array}{l}2sin(x+\frac{π}{3}),x∈[0,π]\\ 2sin(-x+\frac{π}{3}),x∈[-π,0]\end{array}\right.$.
画出f(x)的图象
由图象可以易得f(x)的单调增区间为[-π,-$\frac{π}{6}$]和[0,$\frac{π}{6}$].--------(6分)
(2)方程等价于f(x)=0或f(x)=$\sqrt{3}$,
当x=$±\frac{2}{3}π$时f(x)=0;
当0或$±\frac{1}{3}π$时f(x)=$\sqrt{3}$
综上可知x的所有可能取值为0,$±\frac{1}{3}π$,$±\frac{2}{3}π$--------------(12分)
点评 本题考查的知识点是正弦型函数的图象和性质,函数的图象,熟练掌握正弦型函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
6.已知tan(π-α)=-2,则$\frac{1}{{cos2α+{{cos}^2}α}}$=( )
| A. | -3 | B. | $\frac{2}{5}$ | C. | 3 | D. | $-\frac{5}{2}$ |
20.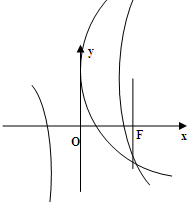 如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
 如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )| A. | $\sqrt{2}$+1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$-1 |
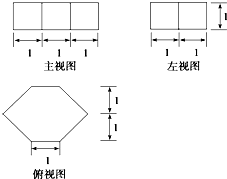
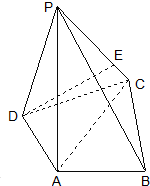 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1,点E在棱PC上,且DE⊥PB.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1,点E在棱PC上,且DE⊥PB.