题目内容
设定义在R的函数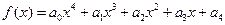 ,
,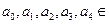 R. 当
R. 当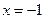 时,
时,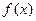 取得极大值
取得极大值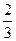 ,且函数
,且函数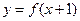 的图象关于点
的图象关于点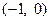 对称.
对称.
(I)求函数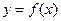 的表达式;
的表达式;
(II)判断函数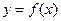 的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间
的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间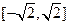 上,并说明理由;
上,并说明理由;
 (III)设
(III)设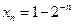 ,
,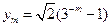 (
(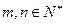 ),求证:
),求证: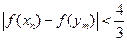 .
.
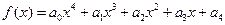 ,
,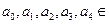 R. 当
R. 当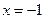 时,
时,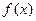 取得极大值
取得极大值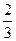 ,且函数
,且函数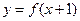 的图象关于点
的图象关于点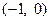 对称.
对称.(I)求函数
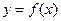 的表达式;
的表达式;(II)判断函数
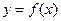 的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间
的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间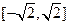 上,并说明理由;
上,并说明理由; (III)设
(III)设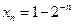 ,
,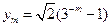 (
(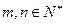 ),求证:
),求证: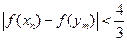 .
.(I)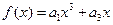 .
.
(II)两点的坐标分别为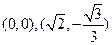 或
或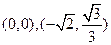 .
.
(III)见解析
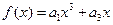 .
.(II)两点的坐标分别为
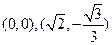 或
或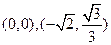 .
.(III)见解析
(I)将函数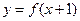 的图象向右平移一个单位得到函数
的图象向右平移一个单位得到函数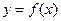 的图象,
的图象,
∴ 函数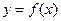 的图象关于点
的图象关于点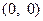 对称,即
对称,即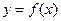 为奇函数.
为奇函数.
∴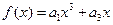 . ……………………………..2分
. ……………………………..2分
由题意可得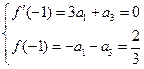 ,解得
,解得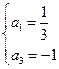 .
.
∴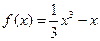 . ……………………………..4分
. ……………………………..4分
 (II)存在满足题意的两点. ……………………………..6分
(II)存在满足题意的两点. ……………………………..6分
由(I)得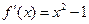 .
.
假设存在两切点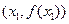 ,
,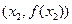 ,且
,且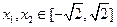 .
.
则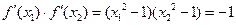 .
.
∵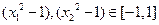 ,∴
,∴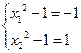 或
或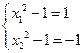 ,
,
即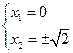 或
或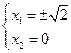 .
.
从而可求得两点的坐标分别为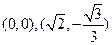 或
或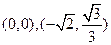 .
.
…………………………….9分
(III)∵当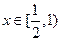 时,
时,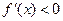 ,∴
,∴ 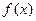 在
在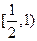 上递减.
上递减.
由已知得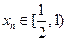 ,∴
,∴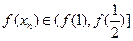 ,即
,即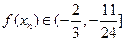 .
.
……………………………..11分
又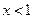 时,
时,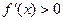 ;
;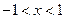 时,
时,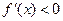 ,
,
∴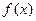 在
在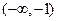 上递增,
上递增,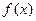 在
在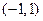 上递减.
上递减.
∵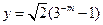 ,∴
,∴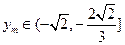 .
.
∵ ,且
,且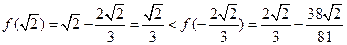 ,
,
∴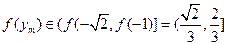 . ……………………………13分
. ……………………………13分
 ∴
∴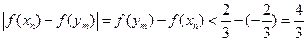 . ………………………..14分
. ………………………..14分
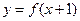 的图象向右平移一个单位得到函数
的图象向右平移一个单位得到函数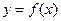 的图象,
的图象, ∴ 函数
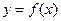 的图象关于点
的图象关于点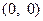 对称,即
对称,即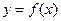 为奇函数.
为奇函数. ∴
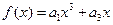 . ……………………………..2分
. ……………………………..2分由题意可得
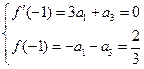 ,解得
,解得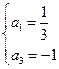 .
. ∴
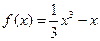 . ……………………………..4分
. ……………………………..4分 (II)存在满足题意的两点. ……………………………..6分
(II)存在满足题意的两点. ……………………………..6分由(I)得
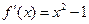 .
. 假设存在两切点
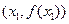 ,
,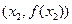 ,且
,且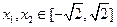 .
.则
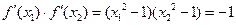 .
. ∵
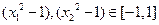 ,∴
,∴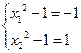 或
或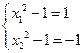 ,
,即
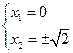 或
或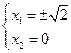 .
. 从而可求得两点的坐标分别为
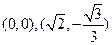 或
或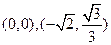 .
.…………………………….9分
(III)∵当
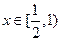 时,
时,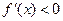 ,∴
,∴ 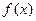 在
在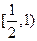 上递减.
上递减.由已知得
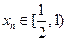 ,∴
,∴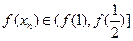 ,即
,即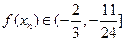 .
.……………………………..11分
又
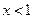 时,
时,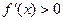 ;
;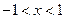 时,
时,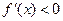 ,
,∴
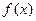 在
在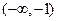 上递增,
上递增,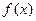 在
在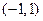 上递减.
上递减.∵
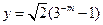 ,∴
,∴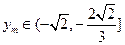 .
. ∵
 ,且
,且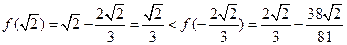 ,
,∴
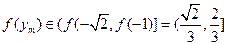 . ……………………………13分
. ……………………………13分  ∴
∴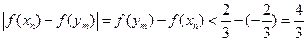 . ………………………..14分
. ………………………..14分
练习册系列答案
相关题目
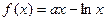 ,
,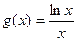 ,它们的定义域都是
,它们的定义域都是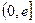 ,其中
,其中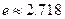 ,
,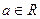
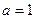 时,求函数
时,求函数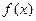 的单调区间;
的单调区间;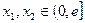 ,求证:
,求证: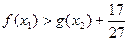
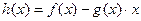 ,问是否存在实数
,问是否存在实数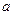 使得
使得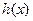 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出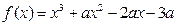
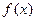 在
在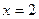 处的切线与直线
处的切线与直线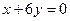 垂直,求
垂直,求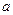 的值
的值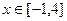 ,使得
,使得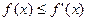 成立
成立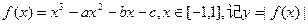 的最大值为M。
的最大值为M。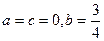 时,求M的值。
时,求M的值。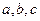 取遍所有实数时,求M的最小值
取遍所有实数时,求M的最小值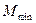 ;
;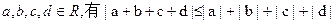 ,当
,当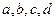 同号时取等号)
同号时取等号)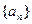 满足
满足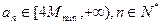 ,求证:
,求证: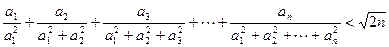 。
。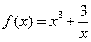 ,求函数f(x)的单调区间及其极值.
,求函数f(x)的单调区间及其极值.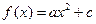 的图象经过点
的图象经过点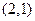 ,且在
,且在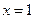 处的切线方程是
处的切线方程是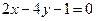
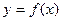 的解析式;
的解析式;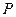 是直线
是直线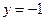 上的动点,自点
上的动点,自点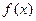 的图象的两条切线
的图象的两条切线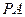 、
、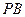 (点
(点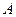 、
、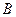 为切点),求证直线
为切点),求证直线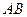 经过一个定点,并求出定点的坐标。
经过一个定点,并求出定点的坐标。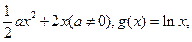
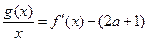 在区间
在区间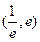 内有且只有两个不相等的实数根?若存在,求出a的取值范围?若不存在,请说明理由。
内有且只有两个不相等的实数根?若存在,求出a的取值范围?若不存在,请说明理由。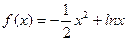 ,
,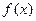 的单调区间;
的单调区间;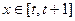
 为大于0的常数),求
为大于0的常数),求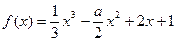 且
且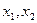 是
是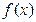 的两个极值点,
的两个极值点,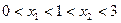 ,
,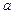 的取值范围;
的取值范围;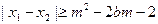 ,对
,对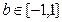 恒成立。求实数
恒成立。求实数 的取值范围;
的取值范围;