题目内容
(本小题满分14分)
已知函数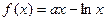 ,
,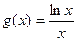 ,它们的定义域都是
,它们的定义域都是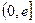 ,其中
,其中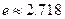 ,
,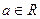
(Ⅰ)当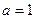 时,求函数
时,求函数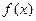 的单调区间;
的单调区间;
(Ⅱ)当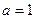 时,对任意
时,对任意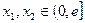 ,求证:
,求证: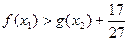
(Ⅲ)令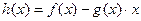 ,问是否存在实数
,问是否存在实数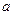 使得
使得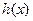 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出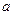 的值;如果不存在,说明理由。
的值;如果不存在,说明理由。
已知函数
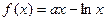 ,
,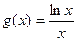 ,它们的定义域都是
,它们的定义域都是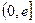 ,其中
,其中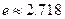 ,
,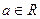
(Ⅰ)当
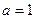 时,求函数
时,求函数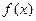 的单调区间;
的单调区间;(Ⅱ)当
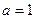 时,对任意
时,对任意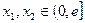 ,求证:
,求证: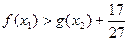
(Ⅲ)令
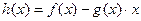 ,问是否存在实数
,问是否存在实数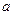 使得
使得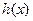 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出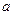 的值;如果不存在,说明理由。
的值;如果不存在,说明理由。(Ⅰ)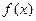 的单调增区间为
的单调增区间为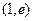 ,减区间为
,减区间为

(Ⅱ)证明见解析。
(Ⅲ)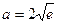
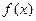 的单调增区间为
的单调增区间为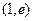 ,减区间为
,减区间为

(Ⅱ)证明见解析。
(Ⅲ)
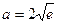
21 (本小题满分14 分)
分)
(Ⅰ)当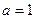 时,
时,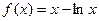 ,
,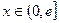
∴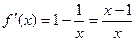 -----------2分
-----------2分
令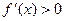 ∴
∴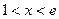 令
令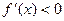 ∴
∴
∴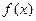 的单调增区间为
的单调增区间为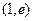 ,减区间为
,减区间为
 -----------4分
-----------4分
(Ⅱ)由(I)知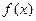 在
在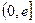 的最小值为
的最小值为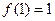 -----
----- ------5分
------5分
又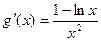
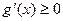 在区间
在区间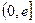 上成立
上成立
∴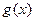 在
在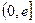 单调递增,故
单调递增,故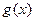 在区间
在区间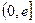 上有最大值
上有最大值 -----------7分
-----------7分
要证对任意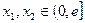 ,
,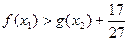
即证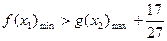
即证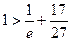 ,即证
,即证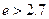
故命题成立 -----------9分
(Ⅲ)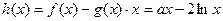 ,
,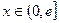
∴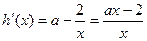
(1)当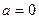 时,
时,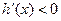 ,∴
,∴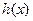 在
在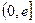 单调递减,
单调递减,
故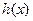 的最小值为
的最小值为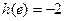 ,舍去 ----
,舍去 ---- -------11分
-------11分
(2)当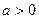 时,由
时,由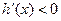 ,得
,得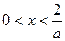
①当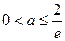 时,
时,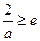 ,
,
∴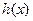 在
在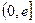 单调递减,故
单调递减,故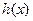 的最小值为
的最小值为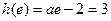 ,
,
∴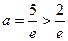 ,舍去
,舍去
②当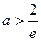 时,
时,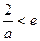 ,
,
∴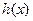 在
在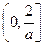 单调递减,在
单调递减,在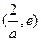 单调递增,
单调递增,
故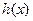 的最小值为
的最小值为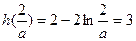 ,
,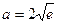 ,满足要求 -----------12分
,满足要求 -----------12分
(3)当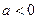 时,
时,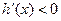 在
在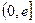 上成立,
上成立,
∴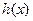 在
在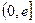 单调递减,故
单调递减,故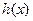 的最小值为
的最小值为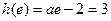 ∴
∴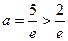 ,舍去
,舍去
综合上述,满足要求的实数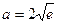 -----------14分
-----------14分
 分)
分)(Ⅰ)当
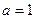 时,
时,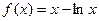 ,
,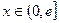
∴
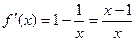 -----------2分
-----------2分令
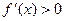 ∴
∴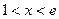 令
令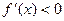 ∴
∴
∴
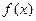 的单调增区间为
的单调增区间为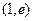 ,减区间为
,减区间为
 -----------4分
-----------4分(Ⅱ)由(I)知
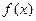 在
在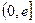 的最小值为
的最小值为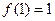 -----
----- ------5分
------5分又
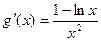
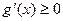 在区间
在区间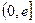 上成立
上成立∴
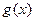 在
在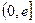 单调递增,故
单调递增,故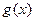 在区间
在区间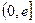 上有最大值
上有最大值 -----------7分
-----------7分要证对任意
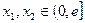 ,
,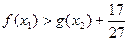
即证
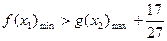
即证
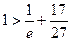 ,即证
,即证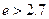
故命题成立 -----------9分
(Ⅲ)
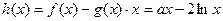 ,
,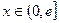
∴
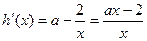
(1)当
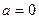 时,
时,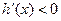 ,∴
,∴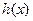 在
在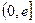 单调递减,
单调递减,故
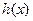 的最小值为
的最小值为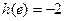 ,舍去 ----
,舍去 ---- -------11分
-------11分(2)当
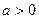 时,由
时,由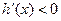 ,得
,得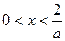
①当
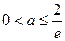 时,
时,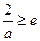 ,
,∴
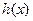 在
在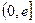 单调递减,故
单调递减,故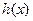 的最小值为
的最小值为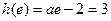 ,
,∴
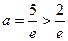 ,舍去
,舍去②当
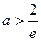 时,
时,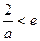 ,
,∴
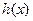 在
在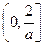 单调递减,在
单调递减,在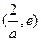 单调递增,
单调递增,故
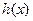 的最小值为
的最小值为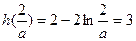 ,
,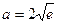 ,满足要求 -----------12分
,满足要求 -----------12分(3)当
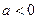 时,
时,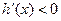 在
在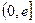 上成立,
上成立,∴
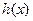 在
在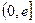 单调递减,故
单调递减,故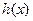 的最小值为
的最小值为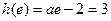 ∴
∴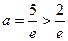 ,舍去
,舍去综合上述,满足要求的实数
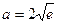 -----------14分
-----------14分
练习册系列答案
相关题目
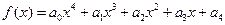 ,
,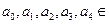 R. 当
R. 当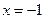 时,
时,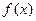 取得极大值
取得极大值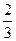 ,且函数
,且函数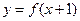 的图象关于点
的图象关于点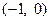 对称.
对称.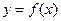 的表达式;
的表达式;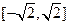 上,并说明理由;
上,并说明理由; (III)设
(III)设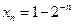 ,
,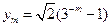 (
(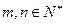 ),求证:
),求证: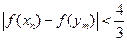 .
.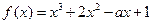 .
.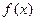 在点
在点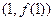 处的切线斜率为4,求实数
处的切线斜率为4,求实数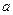 的值;
的值;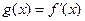 在区间
在区间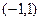 上存在零点,求实数
上存在零点,求实数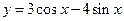 的导数为 .
的导数为 . 则a的值等于 ( )
则a的值等于 ( )



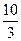
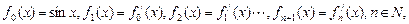 则
则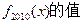

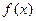 是R上的可导函数,且
是R上的可导函数,且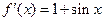 ,则函数
,则函数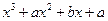 在x=1处取得极值(a>0)
在x=1处取得极值(a>0)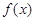 (
(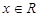 )满足
)满足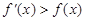 ,则当
,则当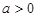 时,
时,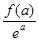 和
和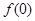 的大小关系为
的大小关系为