题目内容
已知函数f(x)=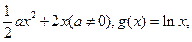
(1)若h(x)=f(x)-g(x)存在单调增区间,求a的取值范围;
(2)是否存在实数a>0,使得方程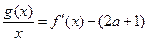 在区间
在区间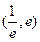 内有且只有两个不相等的实数根?若存在,求出a的取值范围?若不存在,请说明理由。
内有且只有两个不相等的实数根?若存在,求出a的取值范围?若不存在,请说明理由。
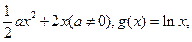
(1)若h(x)=f(x)-g(x)存在单调增区间,求a的取值范围;
(2)是否存在实数a>0,使得方程
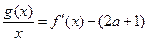 在区间
在区间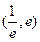 内有且只有两个不相等的实数根?若存在,求出a的取值范围?若不存在,请说明理由。
内有且只有两个不相等的实数根?若存在,求出a的取值范围?若不存在,请说明理由。(Ⅰ) a的取值范围是(-1, 0)∪(0, +∞) (Ⅱ)a的取值范围是(1, 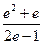 )
)
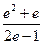 )
)(1)由已知,得h(x)= 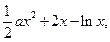 且x>0,
且x>0,
则hˊ(x)=ax+2-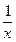 =
=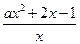 , (2分)
, (2分)
∵函数h(x)存在单调递增区间,
∴hˊ(x)≥0有解, 即不等式ax2+2x-1≥0有x>0的解. (3分)
① 当a<0时, y=ax2+2x-1的图象为开口向下的抛物线, 要使ax2+2x-1≥0总有x>0的解, 则方程ax2+2x-1=0至少有一个不重复正根, 而方程ax2+2x-1=0总有两个不相等的根时, 则必定是两个不相等的正根. 故只需Δ="4+4a>0," 即a>-1. 即-1<a<0(5分)
② 当a>0 时, y= ax2+2x-1的图象为开口向上的抛物线, ax2+2x-1≥0 一定有x>0的解. (6分)
综上, a的取值范围是(-1, 0)∪(0, +∞) (7分)
(2)方程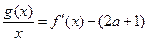
即为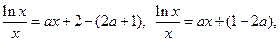
等价于方程ax2+(1-2a)x-lnx="0" . (8分)
设H(x)= ax2+(1-2a)x-lnx, 于是原方程在区间(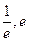 )内根的问题, 转化为函数H(x)在区间(
)内根的问题, 转化为函数H(x)在区间(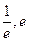 )内的零点问题. (9分)
)内的零点问题. (9分)
Hˊ(x)=2ax+(1-2a)-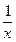 =
= (10分)
(10分)
当x∈(0, 1)时, Hˊ(x)<0, H(x)是减函数;
当x∈(1, +∞)时, Hˊ(x)>0, H(x)是增函数;
若H(x)在(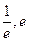 )内有且只有两个不相等的零点, 只须
)内有且只有两个不相等的零点, 只须
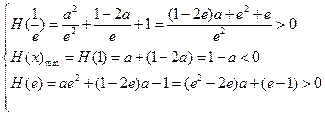 (13分)
(13分)
解得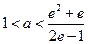 , 所以a的取值范围是(1,
, 所以a的取值范围是(1, 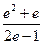 ) (14分)
) (14分)
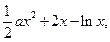 且x>0,
且x>0, 则hˊ(x)=ax+2-
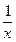 =
=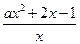 , (2分)
, (2分)∵函数h(x)存在单调递增区间,
∴hˊ(x)≥0有解, 即不等式ax2+2x-1≥0有x>0的解. (3分)
① 当a<0时, y=ax2+2x-1的图象为开口向下的抛物线, 要使ax2+2x-1≥0总有x>0的解, 则方程ax2+2x-1=0至少有一个不重复正根, 而方程ax2+2x-1=0总有两个不相等的根时, 则必定是两个不相等的正根. 故只需Δ="4+4a>0," 即a>-1. 即-1<a<0(5分)
② 当a>0 时, y= ax2+2x-1的图象为开口向上的抛物线, ax2+2x-1≥0 一定有x>0的解. (6分)
综上, a的取值范围是(-1, 0)∪(0, +∞) (7分)
(2)方程
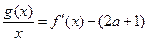
即为
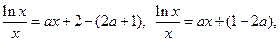
等价于方程ax2+(1-2a)x-lnx="0" . (8分)
设H(x)= ax2+(1-2a)x-lnx, 于是原方程在区间(
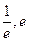 )内根的问题, 转化为函数H(x)在区间(
)内根的问题, 转化为函数H(x)在区间(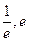 )内的零点问题. (9分)
)内的零点问题. (9分) Hˊ(x)=2ax+(1-2a)-
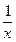 =
= (10分)
(10分)当x∈(0, 1)时, Hˊ(x)<0, H(x)是减函数;
当x∈(1, +∞)时, Hˊ(x)>0, H(x)是增函数;
若H(x)在(
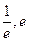 )内有且只有两个不相等的零点, 只须
)内有且只有两个不相等的零点, 只须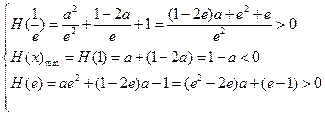 (13分)
(13分)解得
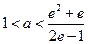 , 所以a的取值范围是(1,
, 所以a的取值范围是(1, 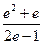 ) (14分)
) (14分)
练习册系列答案
相关题目
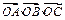 满足
满足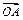 =[f(x)+2f′(1)]
=[f(x)+2f′(1)]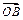 -ln(x+1)
-ln(x+1)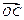
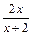 ;
;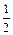 x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围.
x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围.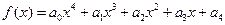 ,
,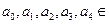 R. 当
R. 当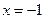 时,
时,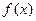 取得极大值
取得极大值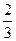 ,且函数
,且函数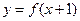 的图象关于点
的图象关于点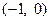 对称.
对称.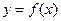 的表达式;
的表达式;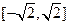 上,并说明理由;
上,并说明理由; (III)设
(III)设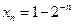 ,
,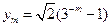 (
(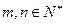 ),求证:
),求证: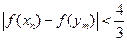 .
.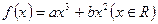 的图像过点P(-1,2),且在点P处的切线恰好与直线
的图像过点P(-1,2),且在点P处的切线恰好与直线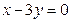 垂直。
垂直。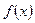 的解析式;
的解析式;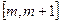 上单调递增,求实数m的取值范围。
上单调递增,求实数m的取值范围。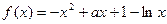 .
.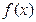 在
在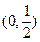 上是减函数,求
上是减函数,求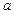 的取值范围;
的取值范围;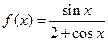 。
。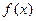 的单调区间;
的单调区间;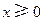 ,都有
,都有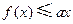 ,求
,求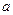 的取值范围。
的取值范围。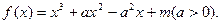
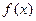 在
在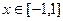 内没有极值点,求
内没有极值点,求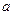 的取值范围。
的取值范围。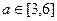 ,不等式
,不等式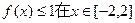 上恒成立,求实数
上恒成立,求实数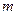 的取值范围。
的取值范围。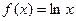 ,
,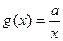 ,设
,设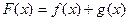 .
.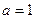 时,求函数
时,求函数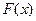 的单调区间;
的单调区间;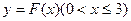 图象上任意一点
图象上任意一点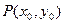 为切点的切线斜率
为切点的切线斜率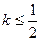 恒成立,求实数
恒成立,求实数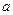 的最小值.
的最小值. 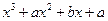 在x=1处取得极值(a>0)
在x=1处取得极值(a>0)