题目内容
9.已知2ax2+bx-3a+1≥0,在x∈[-4,4]上恒成立,求5a+b的最小值.分析 由2ax2+bx-3a+1≥0在x∈[-4,4]上恒成立,得a≤$\frac{1}{3}$,再分类讨论,利用线性规划知识求解,即可求出5a+b的最小值.
解答 解:由2ax2+bx-3a+1≥0恒成立,得a≤$\frac{1}{3}$.
①0<a≤$\frac{1}{3}$时,问题等价于$\left\{\begin{array}{l}{-\frac{b}{4a}≤-4}\\{f(-4)≥0}\end{array}\right.$(1)或$\left\{\begin{array}{l}{-\frac{b}{4a}≥4}\\{f(4)≥0}\end{array}\right.$(2)或f(-$\frac{b}{4a}$)≥0(3).
由(1)得$\left\{\begin{array}{l}{16a-b≤0}\\{29a-4b+1≥0}\end{array}\right.$,对应的区域如图所示,由图知,直线z=5a+b经过点O(0,0)时,取得最小值0;
由(2)得$\left\{\begin{array}{l}{16a+b≤0}\\{29a+4b+1≥0}\end{array}\right.$对应的区域如图所示,由图知,直线z=5a+b经过点A($\frac{1}{35},-\frac{16}{35}$)时,取得最小值-$\frac{11}{35}$
由(3)得24a2-8a+b2≤0,对应的区域如图所示,由图知,直线z=5a+b经过点B($\frac{1}{21},-\frac{12}{21}$)时,取得最小值-$\frac{1}{3}$;
②a≤0时,问题等价于$\left\{\begin{array}{l}{f(-4)≥0}\\{f(4)≥0}\end{array}\right.$,即$\left\{\begin{array}{l}{29a-4b+1≥0}\\{29a+4b+1≥0}\end{array}\right.$,对应的区域如图所示,由图知,直线z=5a+b经过点C(0,-$\frac{1}{4}$)时,取得最小值-$\frac{1}{4}$,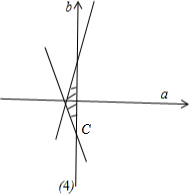
综上,a=$\frac{1}{21}$,b=-$\frac{12}{21}$时,取得最小值-$\frac{1}{3}$.
点评 本题考查恒成立问题,考查学生分析解决问题的能力,考查学生的计算能力,体现了分类讨论的数学思想方法,属于难题.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{3\sqrt{10}}{10}$ |
 已知三棱柱ABC-A1B1C1,O、O1为棱AB、A1B1的中点,OC1=O1C,且CB=CC1=CA.
已知三棱柱ABC-A1B1C1,O、O1为棱AB、A1B1的中点,OC1=O1C,且CB=CC1=CA.



