题目内容
3.若F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>2b>0)的两个焦点,分别过F1,F2作倾斜角为45°的两条直线与椭圆相交于四点,以该四点为顶点的四边形和一椭圆的四个顶点为顶点的四边形的面积比等于$\frac{2\sqrt{2}}{3}$,求该椭圆的离心率( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{3\sqrt{10}}{10}$ |
分析 由点斜式方程求出过F1(-c,0)的直线方程,设直线y=x+c与椭圆的交点为A(x1,y1),B(x2,y2),代入椭圆方程化简后利用韦达定理求出|y1-y2|,由条件列出方程化简,利用椭圆基本量的关系和离心率公式求出e即可.
解答 解:由题意得,过F1(-c,0)倾斜角是45°的直线方程是y=x+c,如图: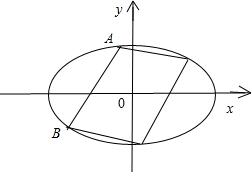
设直线y=x+c与椭圆的交点为A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{y=x+c}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$得,(a2+b2)y2-2b2cy-b4=0,
则y1+y2=$\frac{2{b}^{2}c}{{a}^{2}+{b}^{2}}$,${y}_{1}{y}_{2}=-\frac{{b}^{4}}{{a}^{2}+{b}^{2}}$,
∴$({y}_{1}{-y}_{2})^{2}$=${({y}_{1}{+y}_{2})}^{2}-4{y}_{1}{y}_{2}$=$(\frac{2{b}^{2}c}{{a}^{2}+{b}^{2}})^{2}-4×(-\frac{{b}^{4}}{{a}^{2}+{b}^{2}})$=$\frac{8{a}^{2}{b}^{4}}{{(a}^{2}+{b}^{2})^{2}}$,
则|y1-y2|=$\frac{2\sqrt{2}{ab}^{2}}{{a}^{2}+{b}^{2}}$,
∴以该四点为顶点的四边形的面积S1=|F1F2||y1-y2|=2c•$\frac{2\sqrt{2}{ab}^{2}}{{a}^{2}+{b}^{2}}$=$\frac{4\sqrt{2}{acb}^{2}}{{a}^{2}+{b}^{2}}$,
∵椭圆的四个顶点为顶点的四边形的面积是S2=2ab,
∴$\frac{\sqrt{2}bc}{{a}^{2}+{b}^{2}}=\frac{2\sqrt{2}}{3}$,化简得2b2+c2=3bc,
(2b-c)(b-c)=0,2b=c或b=c;
∴a2=b2+4b2=5b2或a2=2b2,
又∵a>2b>0,∴a2=5b2,则c2=4b2,
∴e=$\frac{c}{a}$=$\frac{2b}{\sqrt{5}b}$=$\frac{2\sqrt{5}}{5}$,
故选:B.
点评 本题考查椭圆的离心率,以及圆锥曲线与直线的位置关系应用,考查化简、变形能力,属于中档题.

| A. | $2β-α=\frac{π}{2}$ | B. | $2β+α=\frac{π}{2}$ | C. | $2β-α=-\frac{π}{2}$ | D. | $2β+α=-\frac{π}{2}$ |
| A. | 焦点在x轴上的椭圆 | B. | 焦在点y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 焦点在y轴上的双曲线 |
| A. | 横坐标缩短到原来的$\frac{1}{3}$倍,纵坐标不变 | |
| B. | 横坐标伸长到原来的3倍,纵坐标不变 | |
| C. | 纵坐标伸长到原来的3倍,横坐标不变 | |
| D. | 纵坐标缩短到原来的$\frac{1}{3}$倍,横坐标不变 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |