题目内容
8.在正方体ABCD-A1B1C1D1中,点 P为正方形A1B1C1D1的中心.下列说法正确的是①②③④(写出你认为正确的所有命题的序号).
①直线AP与平面ABB1A1所成角的正切值为$\frac{\sqrt{5}}{5}$;
②若M,N分别是正方形CDD1C1,BCC1B1的中心,则AP⊥MN;
③若M,N分别是正方形CDD1C1,BCC1B1的中心,则VA-PMN=VN-ACD;
④平面BCC1B1中不存在使$\overrightarrow{MA}$•$\overrightarrow{MP}$=0成立的M点.
分析 如图所示,不妨取AB=2.
①取A1B1的中点E,连接EP,AE.由正方体的性质可得:EP⊥平面ABB1A1.则∠EAP是直线AP与平面ABB1A1所成角,利用直角三角形的边角关系即可得出;
②建立如图所示的空间直角坐标系,计算$\overrightarrow{AP}•\overrightarrow{MN}$即可判断出正误;
③VN-ACD=$\frac{1}{3}×{S}_{ACD}•{h}_{N}$,由于△MNP是等边三角形,边长为$\sqrt{2}$,点A到平面MNP的距离hA=$\frac{2}{3}•A{C}_{1}$,可得VA-MNP,即可判断出正误;
④设M(2,2,z)为平面BCC1B1中的任意一点,则$\overrightarrow{MA}$•$\overrightarrow{MP}$=(z-1)2+1≥1>0,即可判断出正误.
解答 解:如图所示,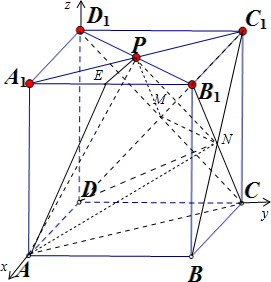 不妨取AB=2.
不妨取AB=2.
①取A1B1的中点E,连接EP,AE.由正方体的性质可得:EP⊥平面ABB1A1.
则∠EAP是直线AP与平面ABB1A1所成角,其正切值=$\frac{EP}{AE}$=$\frac{\sqrt{5}}{5}$,正确;
②建立如图所示的空间直角坐标系,A(2,0,0),P(1,1,2),M(0,1,1),N(1,2,1),
∴$\overrightarrow{AP}$=(-1,1,2),$\overrightarrow{MN}$=(1,1,0),
∴$\overrightarrow{AP}•\overrightarrow{MN}$=-1+1+0=0,∴$\overrightarrow{AP}⊥\overrightarrow{MN}$,即AP⊥MN,正确;
③VN-ACD=$\frac{1}{3}×{S}_{ACD}•{h}_{N}$=$\frac{1}{3}×\frac{1}{2}×{2}^{2}×1$=$\frac{2}{3}$,由于△MNP是等边三角形,边长为$\sqrt{2}$,点A到平面MNP的距离hA=$\frac{2}{3}•A{C}_{1}$=$\frac{2}{3}×2\sqrt{3}$=$\frac{4\sqrt{3}}{3}$,∴VA-MNP=$\frac{1}{3}×\frac{\sqrt{3}}{4}×(\sqrt{2})^{2}×\frac{4\sqrt{3}}{3}$=$\frac{2}{3}$,∴VA-PMN=VN-ACD;
④设M(2,2,z)为平面BCC1B1中的任意一点,则$\overrightarrow{MA}$•$\overrightarrow{MP}$=(0,-2,-z)•(-1,-1,2-z)=2-z(2-z)=(z-1)2+1≥1>0,因此平面BCC1B1中不存在使$\overrightarrow{MA}$•$\overrightarrow{MP}$=0成立的M点,正确.
故答案为:①②③④.
点评 本题考查了正方体的性质、线面垂直的性质、三棱锥的体积计算公式、数量积运算与向量垂直的关系、简易逻辑的判定方法,考查了空间想象能力、推理能力与计算能力,属于中档题.

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | 1 |
| 学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
| 甲班 | 6 | 5 | 7 | 9 | 8 |
| 乙班 | 4 | 8 | 9 | 7 | 7 |
(2)在本次比赛中,从两班中分别任选一个同学,比较两人的射中次数.求甲班同学射中次数高于乙班同学射中次数的概率.
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
| A. | 一组数据2,5,3,1,4,3的中位数是3 | |
| B. | 五边形的外角和是540度 | |
| C. | “菱形的对角线互相垂直”的逆命题是真命题 | |
| D. | 三角形的外心是这个三角形三条角平分线的交点 |