题目内容
19. 已知三棱柱ABC-A1B1C1,O、O1为棱AB、A1B1的中点,OC1=O1C,且CB=CC1=CA.
已知三棱柱ABC-A1B1C1,O、O1为棱AB、A1B1的中点,OC1=O1C,且CB=CC1=CA.(1)证明:平面ABB1A1⊥平面C1COO1;
(2)若OB1=OA1,∠CBA=30°,求二面角C1-OB1-A的余弦值.
分析 (1)利用等腰三角形得出OC∥O1C1,OC⊥AB,根据平行四边形对角线相等得出四边形OCC1O1为矩形,即可判断为AA1⊥OC,再转换为直线与直线的垂直,直线平面的垂直证明即可得出面面垂直.
(2)建立空间坐标系得出点的坐标,根据二面角的余弦值与平面度法向量的夹角的关系求解即可.注意准确求解平面度法向量,充分利用数量积求解.
解答 证明:(1)∵三棱柱ABC-A1B1C1,CB=CC1=CA.
O、O1为棱AB、A1B1的中点,
∴△ABC,△A1B1C1等腰三角形,
∴OC∥O1C1,OC⊥AB,
∵OC1=O1C,AA1∥CC1
∴四边形OCC1O1为矩形,
∴AA1⊥OC,
∴OC⊥面AA1B1B,
∵OC?平面C1COO1,
∴平面ABB1A1⊥平面C1COO1;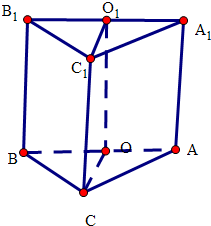
(2)根据(1)可判断三棱柱ABC-A1B1C1为正三棱柱,建立坐标系如图,作EF⊥x轴,
∵OB1=OA1,∠CBA=30°
设BC=1,则EC=$\frac{\sqrt{3}}{2}$,BE=$\frac{1}{2}$,AB=$\sqrt{3}$,
B(0,0,0),O($0,\frac{\sqrt{3}}{2},0$),A(0,$\sqrt{3}$,0),C($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),C1($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,1),B1(0,0,1),
$\overrightarrow{O{B}_{1}}$=(0,$-\frac{\sqrt{3}}{2}$,1),$\overrightarrow{OA}$=(0,$\frac{\sqrt{3}}{2}$,0),$\overrightarrow{O{C}_{1}}$=($\frac{1}{2}$,0,1),
设平面OB1C1的法向量为$\overrightarrow{{n}_{1}}$=(x,y,z),
∴$\left\{\begin{array}{l}{\overrightarrow{O{B}_{1}}•\overrightarrow{{n}_{1}}=0}\\{\overrightarrow{O{C}_{1}}•\overrightarrow{{n}_{1}}=0}\end{array}\right.$即$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{2}y+z=0}\\{\frac{1}{2}x+z=0}\end{array}\right.$
令x=$-2\sqrt{3}$,y=2,z=$\sqrt{3}$,
∴$\overrightarrow{{n}_{1}}$=(-2$\sqrt{3}$,2,$\sqrt{3}$),
设平面OB1A的法向量为$\overrightarrow{{n}_{2}}$=(x,y,z),
根据几何图形判断BE⊥x轴
∴$\overrightarrow{{n}_{2}}$∥$\overrightarrow{BE}$
∴可设$\overrightarrow{{n}_{1}}$=(1,0,0),
∵$\overrightarrow{{n}_{1}}$$•\overrightarrow{{n}_{2}}$=-2$\sqrt{3}$,
∴cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$>=$\frac{-2\sqrt{3}}{\sqrt{19}×1}$=$-\frac{2\sqrt{57}}{19}$.
∵二面角C1-OB1-A的时锐二面角,
∴二面角C1-OB1-A的余弦值$\frac{2\sqrt{57}}{19}$
点评 本题综合考查了空间几何体的性质空间直线平面的位置关系,夹角的求解,考查学生的空间几何能力,运用算能力,计算能力.

| A. | fp[f(0)]=f[fp(0)] | B. | fp[f(1)]=f[fp(1)] | C. | fp[fp(2)]=f[f(2)] | D. | fp[f(3)]=f[f(3)] |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |