题目内容
7.若函数f(x)=-lnx+ax2+bx-a-2b有两个极值点x1,x2,其中-$\frac{1}{2}<a<0$,b>0,且f(x2)=x2>x1,则方程2a[f(x)]2+bf(x)-1=0的实根个数为5.分析 由函数f(x)=-lnx+ax2+bx-a-2b有两个极值点x1,x2,可得2ax2+bx-1=0有两个不相等的正根,必有△=b2+8a>0.而方程2a(f(x))2+bf(x)-1=0的△1=△>0,可知此方程有两解且f(x)=x1或x2.再分别讨论利用平移变换即可解出方程f(x)=x1或f(x)=x2解的个数.
解答 解:∵函数f(x)=-lnx+ax2+bx-a-2b有两个极值点x1,x2,
∴f′(x)=-$\frac{1}{x}$+2ax+b=$\frac{2a{x}^{2}+bx-1}{x}$,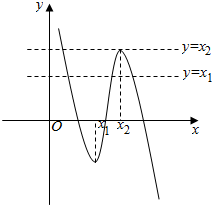
即为2ax2+bx-1=0有两个不相等的正根,
∴△=b2+8a>0.解得x=$\frac{-b±\sqrt{{b}^{2}+8a}}{4a}$.
∵x1<x2,-$\frac{1}{2}<a<0$,b>0,
∴x1=$\frac{-b+\sqrt{{b}^{2}+8a}}{4a}$,x2=$\frac{-b-\sqrt{{b}^{2}+8a}}{4a}$.
而方程2a(f(x))2+bf(x)-1=0的△1=△>0,
∴此方程有两解且f(x)=x1或x2
即有0<x1<x2,:∵x1,x2>0又x1x2=-$\frac{1}{2a}$>1
∴x2>1,∵f(1)=-b<0∴f(x1)<0,
f(x2)>0.
①根据f′(x)画出f(x)的简图,
∵f(x2)=x2,由图象可知方程f(x)=x2有两解,方程f(x)=x1有三解.
综上①②可知:方程f(x)=x1或f(x)=x2共有5个实数解.
即关于x的方程2a(f(x))2+bf(x)-1=0的共有5不同实根.
故答案为:5.
点评 本题综合考查了利用导数研究函数得单调性、极值及方程解得个数、平移变换等基础知识,考查了图象平移的思想方法、推理能力、计算能力、分析问题和解决问题的能力.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案| A. | $\frac{3}{6-4π}$ | B. | $\frac{3}{6-2π}$ | C. | $\frac{3}{6+4π}$ | D. | $\frac{3}{6+2π}$ |
| A. | 横坐标缩短到原来的$\frac{1}{3}$倍,纵坐标不变 | |
| B. | 横坐标伸长到原来的3倍,纵坐标不变 | |
| C. | 纵坐标伸长到原来的3倍,横坐标不变 | |
| D. | 纵坐标缩短到原来的$\frac{1}{3}$倍,横坐标不变 |
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | 1 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |