��Ŀ����
����Ŀ������ˮΧ�������㼼��������ֳ�ܶȸߡ�����Ч��õ��ص㣮�о�����������ˮΧ��������ʱ��ij������һ���������£�ÿβ���ƽ�������ٶ�![]() ����λ��ǧ��/�꣩����ֳ�ܶ�
����λ��ǧ��/�꣩����ֳ�ܶ�![]() ����λ��β/�����ף��ĺ�������
����λ��β/�����ף��ĺ�������![]() ������
������![]() β/������ʱ��
β/������ʱ�� ![]() ��ֵΪ
��ֵΪ![]() ǧ��/�ꣻ��
ǧ��/�ꣻ��![]() ʱ��
ʱ�� ![]() ��
��![]() ��һ�κ������ҵ�
��һ�κ������ҵ�![]() ʱ��
ʱ�� ![]() ��
��
��![]() ����
����![]() ʱ����
ʱ����![]() ����
����![]() �ĺ����ı���ʽ��
�ĺ����ı���ʽ��
��![]() ������ֳ�ܶ�
������ֳ�ܶ�![]() Ϊ���ʱ��ÿ���������������������λ��ǧ��/�����ף����Դﵽ���������ֵ��
Ϊ���ʱ��ÿ���������������������λ��ǧ��/�����ף����Դﵽ���������ֵ��
���𰸡���1��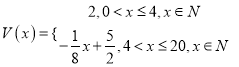 ��2������ֳ�ܶ�Ϊ
��2������ֳ�ܶ�Ϊ![]() β/������ʱ����������������Դﵽ������ֵԼΪ
β/������ʱ����������������Դﵽ������ֵԼΪ![]() ǧ��/�����ף�
ǧ��/�����ף�
�������������������1����������ֶ������ʽ�����ô���ϵ������һ�κ�������ʽ����ֶκ�����ʽ��д��2����һ�κ�������κ������ʷֱ������ֵ�����ȡ�������ֵ
�����������![]() ����
����![]() ʱ��
ʱ�� ![]() ����
����![]() ʱ��
ʱ��
��![]() ����Ȼ�ú���������
����Ȼ�ú���������![]() ���Ǽ�������
���Ǽ�������
����֪��![]() �����
�����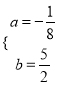 ��
��
�ʺ���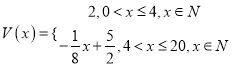 ��
��
��![]() �������Ⲣ�ɣ�
�������Ⲣ�ɣ�![]() ���ɵ�
���ɵ�
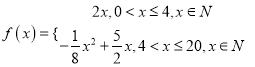 ��
��
��![]() ʱ��
ʱ�� ![]() Ϊ����������
����������![]() ��
��
��![]() ʱ��
ʱ�� ![]() ��
��
![]() ��
��
���ԣ���![]() ʱ��
ʱ�� ![]() �����ֵΪ
�����ֵΪ![]() ��
��
����ֳ�ܶ�Ϊ![]() β/������ʱ����������������Դﵽ���
β/������ʱ����������������Դﵽ���
���ֵԼΪ![]() ǧ��/�����ף�
ǧ��/�����ף�

����Ŀ��ij�����Ϊ�˽����¶�Ӫҵ���Ӱ�죬�����¼�˸õ�1�·���5�����Ӫҵ��y����λ��ǧԪ����õص����������x����λ���棩�����ݣ������
x | 2 | 8 | 9 | 11 | 5 |
y | 12 | 8 | 8 | 7 | 10 |
��1����y����x�Ļع鷽�� ![]() ��
��
��2���ж�y��x֮��������ػ��Ǹ���أ����õ�1�·�ij����������Ϊ6�棬������ع鷽��Ԥ��õ굱�յ�Ӫҵ� �������ع鷽�� ![]() �У�
�У� ![]() =
= 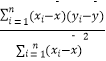 =
= 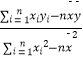 ��
�� ![]() =
= ![]() ��
�� ![]() ����
����