Question

【题目】已知直线a，b和平面M，N，且a⊥M，则下列说法正确的是　(　　)

A. b∥Mb⊥a B. b⊥ab∥M

C. N⊥Ma∥N D. aNM∩N≠

Answer 1

【答案】A

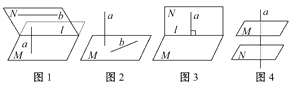
【解析】对于A，如图1所示：过直线b作平面N与平面M相交于直线l，由直线与平面平行的性质定理可知：b∥l，又因为a⊥M，lM，所以a⊥l，所以b⊥a，A正确.选项B，C均少考虑了直线在面内的情况，分别如图2，3所示，均错误；对于D，用排除法，如图4所示，M∥N，D错误;故选A.

点睛:直线与平面的位置关系有:平行,相交和直线在平面内, 直线与平面平行:(1)定义：如果直线a与平面α没有公共点，则直线a与平面α平行;(2)判定定理:平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行． (3)性质定理：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行．